Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
W l k A = ( Z m p + ( A - Z ) m n - m X ) c 2 A ⇔ 7 , 75 = ( 8 . 1 , 0073 + 9 . 1 , 0087 - m X ) 8 + 9 ⇒ m X = 16 , 9953 u

Độ hụt khối của hạt nhân B 4 10 e
4 m p + 6 m n - mBe = 4.1,0073 u + 6.1,0087 u - 10,0135 u = 0,0679 u
Năng lượng liên kết của hạt nhân B 4 10 e là 0,0679.931 = 63,215 MeV
Năng lượng liên kết riêng của hạt nhân B 4 10 e là :
63,215/10 = 6,3215 MeV/ nuclôn

Phương pháp: Năng lượng liên kết riêng ε = Wlk/A = ∆m.c2/A
Cách giải: Năng lượng liên kết riêng của Ar và Li
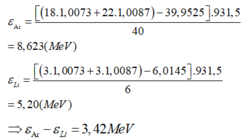
Đáp án B

Đáp án B
Phương pháp: Sử dụng định luật bảo toàn điện tích và số khối để viết phương trình phản ứng
Áp dụng công thức tính năng lượng tỏa ra của phản ứng hạt nhân:
![]()
Trong đó: Wlkt, Wlks lần lượt là năng lượng liên kết của các hạt trước là sau phản ứng.
Cách giải:
Năng lượng tỏa ra:
![]()
![]()
![]()
Chọn B

Năng lượng liên kết riêng của hạt nhân
\(W_{lkr}= \frac{W_{lk}}{A} = \frac{(Zm_p+(A-Z)m_n-m_{Be})c^2}{A}\)
\( = \frac{0,0679.931}{10}= 6,3215MeV.\)

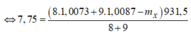
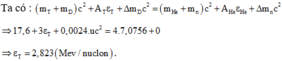
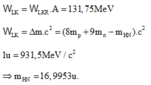
Phương pháp: Sử dụng công thức tính năng lượng liên kết riêng: ε = Wlk/A
Wlk = [Z.mp + (A – Z).mn – m].c2
Cách giải:
Năng lượng liên kết của hạt nhân Be: Wlk = (4.mp + 6.mn – mBe).c2 = 63,2149 (MeV)
Năng lượng liên kết riêng: ε = Wlk/10 = 6,3215 MeV/nuclon
Đáp án D