Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
+ 2x2 + y2 – 8x + 2y – 1 = 0 không phải phương trình đường tròn vì hệ số của x2 khác hệ số của y2.
+ Phương trình x2 + y2 + 2x – 4y – 4 = 0 có :
a = –1; b = 2; c = –4 ⇒ a2 + b2 – c = 9 > 0
⇒ phương trình trên là phương trình đường tròn.
+ Phương trình x2 + y2 – 2x – 6y + 20 = 0 có :
a = 1; b = 3; c = 20 ⇒ a2 + b2 – c = –10 < 0
⇒ phương trình trên không là phương trình đường tròn.
+ Phương trình x2 + y2 + 6x + 2y + 10 = 0 có :
a = –3; b = –1; c = 10 ⇒ a2 + b2 – c = 0 = 0
⇒ phương trình trên không là phương trình đường tròn.
Đáp án D
- Ta có :
(C1) tâm I1(0;2) và R1= 3; (C2) tâm I2( 3;-4) và R2= 3
- Nhận xét : 
không cắt C2
- Gọi d: ax+ by+ c= 0 là tiếp tuyến chung , thế thì : d(I1; d) = R1 và d (I2; d) = R2
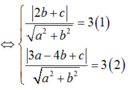
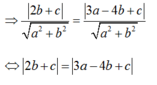
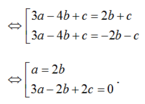
- Trường hợp: a= 2b thay vào (1):
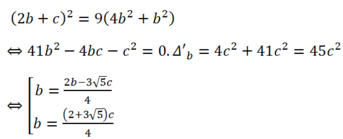
- Do đó ta có hai đường thẳng cần tìm :
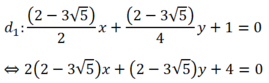
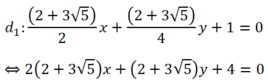
- Trường hợp :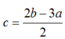 
thay vào :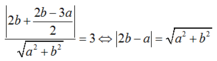 
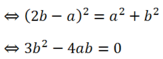
-Có 2 đường thẳng : d3: 2x- 1 = 0 và d4: 6x + 8y -1= 0.
Có tất cả 4 tiếp tuyến chung.
a) x2 + y2 – 4x + 8y – 5 = 0
⇔ (x2 – 4x + 4) + (y2 + 8y + 16) = 25
⇔ (x – 2)2 + (y + 4)2 = 25.
Vậy (C) có tâm I(2 ; –4), bán kính R = 5.
b) Thay tọa độ điểm A vào phương trình đường tròn ta thấy:
(–1 – 2)2 + (0 + 4)2 = 32 + 42 = 52= R2
⇒ A thuộc đường tròn (C)
⇒ tiếp tuyến (d’) cần tìm tiếp xúc với (C) tại A
⇒ (d’) là đường thẳng đi qua A và vuông góc với IA
⇒ (d’) nhận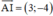 
là một vtpt và đi qua A(–1; 0)
⇒ phương trình (d’): 3(x + 1) – 4(y - 0)= 0 hay 3x – 4y + 3 = 0.
c) Gọi tiếp tuyến vuông góc với (d) : 3x – 4y + 5 = 0 cần tìm là (Δ).
(d) có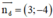 
là một vtpt; 1 VTCP là ud→(4; 3)
(Δ) ⊥ (d) ⇒ (Δ) nhận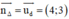 
là một vtpt
⇒ (Δ): 4x + 3y + c = 0.
(C) tiếp xúc với (Δ) ⇒ d(I; Δ) = R
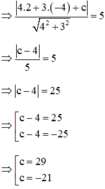
Vậy (Δ) : 4x + 3y + 29 = 0 hoặc 4x + 3y – 21 = 0.
Cách 1 : Xác định các hệ số a, b, c.
a) x2 + y2 – 2x – 2y – 2 = 0 có hệ số a = 1 ; b = 1 ; c = –2
⇒ tâm I (1; 1) và bán kính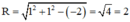 
b) 16x2 + 16y2 + 16x – 8y –11 = 0
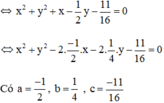
⇒ Đường tròn có tâm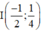 
, bán kính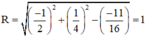 
c) x2 + y2 - 4x + 6y - 3 = 0
⇔ x2 + y2 - 2.2x - 2.(-3).y - 3 = 0
có hệ số a = 2, b = -3,c = -3
⇒ Đường tròn có tâm I(2 ; –3), bán kính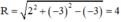 
Cách 2 : Đưa về phương trình chính tắc :
a) x2 + y2 - 2x - 2y - 2 = 0
⇔ (x2 - 2x + 1) + (y2 - 2y +1) = 4
⇔(x-1)2 + (y-1)2 = 4
Vậy đường tròn có tâm I(1 ; 1) và bán kính R = 2.
b) 16x2 + 16y2 + 16x - 8y - 11 = 0
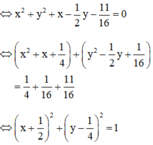
Vậy đường tròn có tâm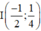 
và bán kính R = 1.
c) x2 + y2 - 4x + 6y -3 = 0
⇔ (x2 - 4x + 4) + (y2 + 6y + 9) = 4 + 9 + 3
⇔ (x - 2)2 + (y + 3)2 = 16
Vậy đường tròn có tâm I( 2 ; –3) và bán kính R = 4.
Áp dụng công thức ta có tâm I(- 1; 4)
Bán kính R = ( − 1 ) 2 + 4 2 − 8 = 3 .
Đáp án C.
Chú ý: Khi học sinh không nhớ công thức của tâm và bán kính thì cần biến đổi phương trình đường tròn ở dạng tổng quát về dạng chính tắc
x 2 + y 2 + 2 x − 8 y + 8 = 0 ⇔ x + 1 2 + y − 4 2 = 9
Từ đó có thông tin về tâm và bán kính của đường tròn.
Các phương án A, B, D là các sai lầm thường gặp của học sinh.
Ta xét các phương án:
(I) có:
(II) có:
(III) tương đương : x2+ y2 – 2x - 3y + 0,5= 0.
phương trình này có:
Vậy chỉ (I) và (III) là phương trình đường tròn.
Chọn D.
a) Đây không phải là dạng của phương trình đường tròn (hệ số \({y^2}\) bằng -1).
b) Vì \({a^2} + {b^2} - c = {1^2} + {\left( { - 2} \right)^2} - 6 < 0\) nên phương trình đã cho không là phương trình tròn.
c) Vì \({a^2} + {b^2} - c = {\left( { - 3} \right)^2} + {2^2} - 1 = 11 > 0\) nên phương trình đã cho là phương trình tròn có tâm \(I\left( { - 3;2} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} - c} = \sqrt {11} \).
Phương trình của (C) là x 2 + y 2 − 6 x + 4 y − 12 = 0 ⇔ x − 3 2 + y + 2 2 = 25
Đường tròn này có tâm I(3; -2) và bán kính R = 5.
Ta có tiếp tuyến tại A(-1; 1): đi qua A, nhận A I → ( 4 ; − 3 ) làm VTPT nên có phương trình:
4(x +1) – 3 (y -1 ) = 0 hay 4x – 3y + 7 = 0 ó - 4x + 3y - 7 = 0
Đáp án A
Tọa độ giao điểm là nghiệm của hệ phương trình
x 2 + y 2 − 6 x − 4 y + 9 = 0 x 2 + y 2 − 2 x − 8 y + 13 = 0 ⇔ x 2 + y 2 − 6 x − 4 y + 9 = 0 − 4 x + 4 y − 4 = 0 ⇔ x 2 + y 2 − 6 x − 4 y + 9 = 0 ( 1 ) x − y + 1 = 0 ( 2 )
Từ (2) suy ra: y = x+ 1 thay vào (1) ta được:
x 2 + ( x + 1 ) 2 - 6 x – 4 ( x + 1 ) + 9 = 0 x 2 + x 2 + 2 x + 1 - 6 x - 4 x – 4 + 9 = 0
2 x 2 – 8 x + 6 = 0
Vậy 2 đường tròn đã cho cắt nhau tại 2 điểm là (1; 2) và (3;4).
ĐÁP ÁN B
a) Đây không phải là phương trình đường tròn do có \(xy\).
b) Vì \({a^2} + {b^2} - c = {1^2} + {2^2} - 5 = 0\)nên phương trình đã cho không là phương trình tròn.
c) Vì \({a^2} + {b^2} - c = {\left( { - 3} \right)^2} + {4^2} - 1 = 24 > 0\)nên phương trình đã cho là phương trình tròn có tâm \(I\left( { - 3;4} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} - c} = 2\sqrt 6 \).