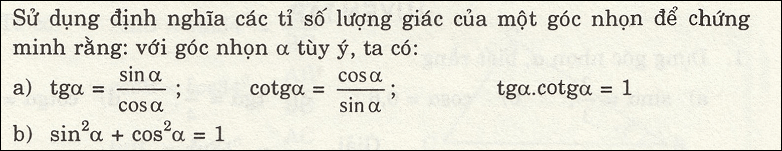Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
\(\cos60^0=\sin30^0;\sin67^0=\cos23^0;\tan80^0=\cot10^0;\cot20^0=\cot20^0\)
Bài 2:
Xét tam giác ABC vuông tại A
\(a,\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{AC}{BC}:\dfrac{AB}{BC}=\dfrac{AC}{AB}=\tan\alpha\\ \cot\alpha=\dfrac{1}{\tan\alpha}=\dfrac{1}{\dfrac{\sin\alpha}{\cos\alpha}}=\dfrac{\cos\alpha}{\sin\alpha}\\ \tan\alpha\cdot\cot\alpha=\dfrac{AC}{AB}\cdot\dfrac{AB}{AC}=1\\ b,\sin^2\alpha+\cos^2\alpha=\dfrac{AC^2}{BC^2}+\dfrac{AB^2}{BC^2}=\dfrac{AB^2+AC^2}{BC^2}=\dfrac{BC^2}{BC^2}=1\left(định.lí.pytago\right)\)


sin75=cos15
cos53=sin37
tan71=cot19
cot47=tan43
sin57 độ 25'=cos 32 độ 35'
tan 68 độ35'=cot 21 độ 25'
cos 87 độ 12 p=sin 2 độ 48'

a, Ta có: cos 88 0 < sin 40 0 (= cos 50 0 ) < cos 28 0 < sin 65 0 (= cos 25 0 ) < cos 20 0
b, Ta có: cot 67 0 18 ' (= tan 22 0 42 ' ) < tan 32 0 48 ' < tan 56 0 32 ' < cot 28 0 36 ' (= tan 61 0 24 ' )

a, Ta có: cos 70 0 (= sin 20 0 ) < sin 24 0 < sin 54 0 < cos 35 0 (= sin 55 0 ) < sin 78 0
b, Ta có: tan 16 0 (= cot 74 0 ) < cot 57 0 67 ' < cot 30 0 < cot 24 0 < tan 80 0 (= cot 10 0 )

\(sin60^0=cos\left(90^0-60^0\right)=cos30^0\)
\(cos75^0=sin\left(90^0-75^0\right)=sin15^0\)
\(cot82^03'=tan\left(90^0-82^03'\right)=tan\left(7^057'\right)\)
\(tan80^0=cot\left(90^0-80^0\right)=cot10^0\)

Sin 15 độ , Sin 30 độ , Cos 58 độ , Sin 48 độ , Cos 36 độ , Có 29 độ
Có phải giải thích ko bạn .
@Nguyễn Thành Trương @Nguyễn Ngọc Lộc giúp cj ý giải bài này với ạ. ( Cj ý nhờ e tag tên giùm; xl vì đã tag tên tự tiện ạ)

\(A=sin42^0-cos48^0=cos\left(90^0-42^0\right)-cos48^0=cos48^0-cos48^0=0\)
\(B=cot56^0-tan34^0=tan\left(90^0-56^0\right)-tan34^0=tan34^0-tan34^0=0\)
\(C=sin30^0-cot50^0-cos60^0+tan40^0\)
\(=cos\left(90^0-30^0\right)-tan\left(90^0-50^0\right)-cos60^0+tan40^0\)
\(=cos60^0-tan40^0-cos60^0+tan40^0=0\)
\(A=\sin42^0-\cos48^0=\sin42^0-\sin42^0=0\)
\(B=\cot56^0-\tan34^0=\tan34^0-\tan34^0=0\)