
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2.
Gọi quãng đường AB là x(km) ( x>0 )
Thời gian đi là \(\dfrac{x}{20}\)
Thời gian về là \(\dfrac{x}{15}\)
Theo đề bài, ta có:
\(\dfrac{x}{15}-\dfrac{x}{20}=\dfrac{1}{6}\)
\(\Leftrightarrow\dfrac{4x-3x}{60}=\dfrac{10}{60}\)
\(\Leftrightarrow x=10\left(tm\right)\)
Vậy quãng đường AB dài 10km


Bài 1:
\(a,\)
\(P=2\left(2x-1\right)^2-\left(x+1\right)^2+3\)
\(=2\left(4x^2-4x+1\right)-\left(x^2+2x+1\right)+3\)
\(=8x^2-8x+2-x^2-2x-1+3\)
\(=7x^2-10x+4\)
\(=7\left(x^2-\dfrac{10}{7}x+\dfrac{4}{7}\right)\)
\(=7\left[x^2-2.x.\dfrac{5}{7}+\left(\dfrac{5}{7}\right)^2-\left(\dfrac{5}{7}\right)^2+\dfrac{4}{7}\right]\)
\(=7\left[\left(x-\dfrac{5}{7}\right)^2+\dfrac{3}{49}\right]\)
\(=7\left(x-\dfrac{5}{7}\right)^2+\dfrac{3}{7}\)
Vì \(7\left(x-\dfrac{5}{7}\right)^2\ge0\forall x\)
\(\Rightarrow7\left(x-\dfrac{5}{7}\right)^2+\dfrac{3}{7}\ge\dfrac{3}{7}\forall x\)
\(\Rightarrow P_{min}=\dfrac{3}{7}\Leftrightarrow7\left(x-\dfrac{5}{7}\right)^2=0\Leftrightarrow x=\dfrac{5}{7}\)
\(b,\)
\(Q=3\left(x+2\right)^2-\left(x-2\right)\left(x+2\right)\)
\(=3\left(x^2+4x+4\right)-\left(x^2-4\right)\)
\(=3x^2+12x+12-x^2+4\)
\(=2x^2+12x+16\)
\(=2\left(x^2+6x+8\right)\)
\(=2\left(x^2+6x+9-1\right)\)
\(=2\left[\left(x+3\right)^2-1\right]\)
\(=2\left(x+3\right)^2-2\)
Vì \(2\left(x+3\right)^2\ge0\forall x\)
\(\Rightarrow2\left(x+3\right)^2-2\ge-2\forall x\)
\(\Rightarrow Q_{min}=-2\Leftrightarrow2\left(x+3\right)^2=0\Leftrightarrow x=-3\)
\(c,\)
Tương tự: \(M=\left(x+1\right)^3-\left(x-2\right)^3-5\)
\(=9x^2-9x+4\)
\(=9\left(x^2-x+\dfrac{4}{9}\right)\)
\(=9\left[x^2-2.x.\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2-\left(\dfrac{1}{2}\right)^2+\dfrac{4}{9}\right]\)
\(=9\left[\left(x-\dfrac{1}{2}\right)^2+\dfrac{7}{36}\right]\)
\(=9\left(x-\dfrac{1}{2}\right)^2+\dfrac{7}{4}\)
Ta có: \(9\left(x-\dfrac{1}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}\forall x\)
\(\Rightarrow M_{min}=\dfrac{7}{4}\Leftrightarrow9\left(x-\dfrac{1}{2}\right)^2=0\Leftrightarrow x=\dfrac{1}{2}\)
Bài 2:
\(a,\)
\(M=-3x^2-4x+1\)
\(=-3\left(x^2+\dfrac{4}{3}x-\dfrac{1}{3}\right)\)
\(=-3\left[x^2+2.x.\dfrac{2}{3}+\left(\dfrac{2}{3}\right)^2-\left(\dfrac{2}{3}\right)^2-\dfrac{1}{3}\right]\)
\(=-3\left[\left(x+\dfrac{2}{3}\right)^2-\dfrac{7}{9}\right]\)
\(=-3\left(x+\dfrac{2}{3}\right)^2+\dfrac{7}{3}\)
Ta có: \(-3\left(x+\dfrac{2}{3}\right)^2\le\dfrac{7}{3}\forall x\)
\(\Rightarrow M_{max}=\dfrac{7}{3}\Leftrightarrow-3\left(x+\dfrac{2}{3}\right)^2=0\Leftrightarrow x=-\dfrac{2}{3}\)
\(b,\)
\(Q=\left(x+2\right)^2-3\left(x-1\right)^2+3\)
\(=-2x^2+10x+4\)
\(=-2\left(x^2-5x-2\right)\)
\(=-2\left[\left(x-\dfrac{5}{2}\right)^2-\dfrac{33}{4}\right]\)
\(=-2\left(x-\dfrac{5}{2}\right)^2+\dfrac{33}{2}\)
Tương tự, \(Q_{max}=\dfrac{33}{2}\Leftrightarrow x=\dfrac{5}{2}\)
\(c,\)
\(P=\left(x-1\right)\left(x+2\right)-2\left(x+3\right)^2\)
\(=-x^2-11x-20\)
\(=-\left(x^2+11x+20\right)\)
\(=-\left(x+\dfrac{11}{2}\right)^2+\dfrac{41}{4}\)
Tương tự, \(Q_{max}=\dfrac{41}{4}\Leftrightarrow x=-\dfrac{11}{2}\)
2:
a: =-3(x^2+4/3x-1/3)
=-3*(x^2+2*x*2/3+4/9-7/9)
=-3(x+2/3)^2+7/3<=7/3
Dấu = xảy ra khi x=-2/3
b: =x^2+4x+4-3x^2+6x-3+3
=-2x^2+10x+4
=-2(x^2-5x-2)
=-2(x^2-5x+25/4-33/4)
=-2(x-5/2)^2+33/2<=33/2
Dấu = xảy ra khi x=5/2
c: =x^2+x-2-2x^2-12x-18
=-x^2-11x-20
=-(x^2+11x+20)
=-(x^2+11x+121/4-41/4)
=-(x+11/2)^2+41/4<=41/4
Dấu = xảy ra khi x=-11/2

2:
a: \(A⋮B\)
=>\(3x^4-12x^3+5x^3-20x^2+31x^2-124x+125x-500+500-a⋮x-4\)
=>500-a=0
=>a=500
b: A chia hết cho B
=>x^4-x^3+5x^2+x^2-x+5+a-5 chia hết cho x^2-x+5
=>a-5=0
=>a=5
1:
a: A chia hết cho B
=>2n-n-3>=0 và 6-n-n>=0
=>n>=3 và n<=3
=>n=3
b: C chia hết cho D
=>9-n>=0 và n+2-9>=0 và n+1-n>=0 và n-9>=0
=>n=9

a: =x^2-2xy+y^2+y^2+4y+4-2
=(x-y)^2+(y+2)^2-2>=-2
Dấu = xảy ra khi x=y=-2
c: =(x+y)^2-4(x+y)+4+1
=(x+y-2)^2+1>=1
Dấu = xảy ra khi x+y=2
b: =x^2-3x+9/4+4y^2-4y+1+23/4
=(x-3/2)^2+(2y-1)^2+23/4>=23/4
Dấu = xảy ra khi x=3/2 và y=1/2


Bài 10:
a: Xét tứ giác AEMF có
AE//MF
AF//ME
Do đó: AEMF là hình bình hành

Bài 1:
\(VT=1\cdot\left(a+b\right)\left(a^2+b^2\right)\left(a^4+b^4\right)\left(a^8+b^8\right)\left(a^{16}+b^{16}\right)\)
\(=\left(a-b\right)\left(a+b\right)\left(a^2+b^2\right)\cdot\left(a^4+b^4\right)\left(a^8+b^8\right)\left(a^{16}+b^{16}\right)\)
\(=\left(a^2-b^2\right)\left(a^2+b^2\right)\left(a^4+b^4\right)\left(a^8+b^8\right)\left(a^{16}+b^{16}\right)\)
\(=\left(a^4-b^4\right)\left(a^4+b^4\right)\left(a^8+b^8\right)\left(a^{16}+b^{16}\right)\)
\(=a^{32}-b^{32}\)



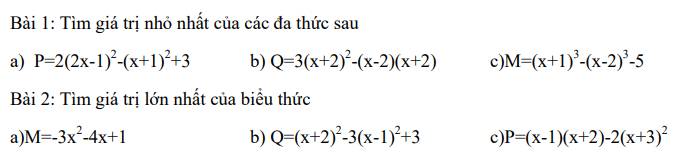



Bài 4:
Ta có: \(\left(4n+3\right)^2-25\)
\(=\left(4n+3-5\right)\left(4n+3+5\right)\)
\(=\left(4n-2\right)\left(4n+8\right)\)
\(=8\left(n+2\right)\left(2n-1\right)⋮8\)
Bài 4:
Ta có: ( 4n + 3 )2 - 25
= ( 4n + 3 - 5 ) . ( 4n + 3 + 5 )
= ( 4n - 2 ) . ( 4n + 8 )
= 8 ( n + 2 ) . ( 2n - 1 ) dấu chia hết 8
Mik ko viết đc dấu chia hết nhé