
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: M(x)+N(x)=7x^3-8x^2-13x-7
b: M(x)+Q(x)=12x^3-2x^2-5x-20
c: N(x)+Q(x)=13x^3-22x-9
d: N(x)-Q(x)=-5x^3-6x^2-8x+13
e: Q(x)-M(x)=6x^3+8x^2-9x-2

A = 3 + 32 + 33 +...+ 32015
A = (3 + 32 + 33 + 34 + 35) +...+ (32011 + 32012 + 32013 + 32014 + 32015)
A = 3.( 1 + 3 + 32 + 33 + 34) +...+ 32011( 1 + 3 + 32 + 33 + 34 )
A = 3.211 +...+ 32011.121
A = 121.( 3 +...+ 32021)
121 ⋮ 121 ⇒ A = 121 .( 3 +...+32021) ⋮ 121 (đpcm)
b, A = 3 + 32 + 33 + 34 +...+ 32015
3A = 32 + 33 + 34 +...+ 32015 + 32016
3A - A = 32016 - 3
2A = 32016 - 3
2A + 3 = 32016 - 3 + 3
2A + 3 = 32016 = 27n
27n = 32016
(33)n = 32016
33n = 32016
3n = 2016
n = 2016 : 3
n = 672
c, A = 3 + 32 + ...+ 32015
A = 3.( 1 + 3 +...+ 32014)
3 ⋮ 3 ⇒ A = 3.(1 + 3 + 32 +...+ 32014) ⋮ 3
Mặt khác ta có: A = 3 + 32 +...+ 32015
A = 3 + (32 +...+ 32015)
A = 3 + 32.( 1 +...+ 32015)
A = 3 + 9.(1 +...+ 32015)
9 ⋮ 9 ⇒ 9.(1 +...+ 32015) ⋮ 9
3 không chia hết cho 9 nên
A không chia hết cho 9, mà A lại chia hết cho 3
Vậy A không phải là số chính phương vì số chính phương chia hết cho số nguyên tố thì sẽ chia hết cho bình phương số nguyên tố đó. nhưng A ⋮ 3 mà không chia hết cho 9

Bạn ơi , bạn xem lại đề nhé! Mình làm thế này không biết có đúng đề không nữa?
Ta có \(a^2+c^2\ge0\) (gt) mà \(a^2\ge0 \forall a, c^2\ge0 \forall c\)=> \(a\ne0 , c\ne0\)=> \(b\ne0\)( vì \(ab=c^2\))
Với \(a,b,c \ne0\), \(ab=c^2\)=> \(\frac{a}{c}=\frac{c}{b}\)
=> \(\left(\frac{a}{c}\right)^2=\left(\frac{c}{b}\right)^2\)
=> \(\frac{a^2}{c^2}=\frac{c^2}{b^2}=\frac{a^2+c^2}{c^2+b^2}\) mà \(\frac{a}{c}=\frac{c}{b}\)
=> \(\frac{a^2+c^2}{c^2+b^2}=\frac{a}{c}.\frac{c}{b}=\frac{a}{b}\)


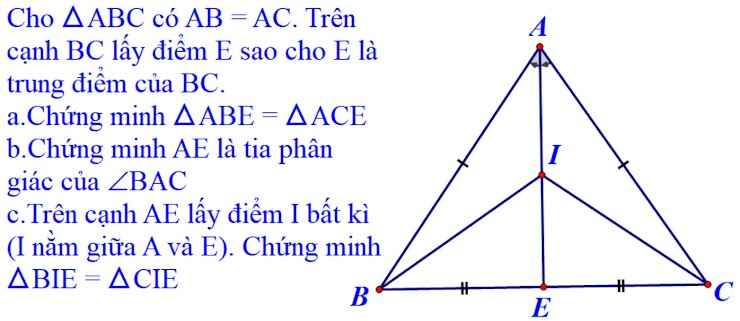
a) Xét tam giác ABE và tam giác ACE có:
+ AE chung.
+ AB = AC (gt).
+ BE = CE (E là trung điểm của BC).
=> Tam giác ABE = Tam giác ACE (c - c - c).
b) Xét tam giác ABC có: AB = AC (gt).
=> Tam giác ABC cân tại A.
Mà AE là đường trung tuyến (E là trung điểm của BC).
=> AE là phân giác ^BAC (Tính chất các đường trong tam giác cân).
c) Xét tam giác ABC cân tại A có:
AE là phân giác ^BAC (cmt).
=> AE là đường cao (Tính chất các đường trong tam giác cân).
=> AE \(\perp\) BC.
Xét tam giác BIE và tam giác CIE:
+ IE chung.
+ BE = CE (E là trung điểm của BC).
+ ^BEI = ^CEI ( = 90o).
=> Tam giác BIE = Tam giác CIE (c - g - c).

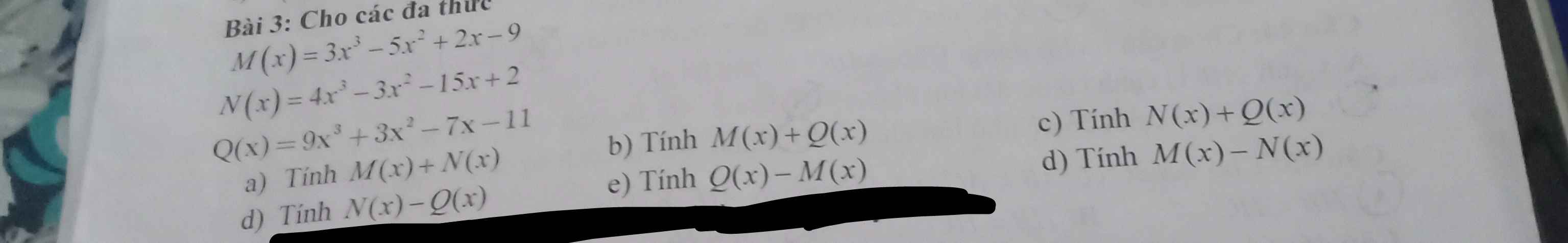

Bài 5*:
\(E\inℤ\Rightarrow2E=\frac{2x+2}{2x+1}=\frac{2x+1+1}{2x+1}=1+\frac{1}{2x+1}\inℤ\Leftrightarrow\frac{1}{2x+1}\inℤ\)
mà \(x\inℤ\Leftrightarrow2x+1\inƯ\left(1\right)=\left\{-1,1\right\}\)
\(\Leftrightarrow x\in\left\{-1,0\right\}\).
Thử lại đều thỏa mãn.
Bài 1:
\(A=\frac{x+15}{x-2}=\frac{x-2+17}{x-2}=1+\frac{17}{x-2}\inℤ\Leftrightarrow\frac{17}{x-2}\inℤ\)
mà \(x\)là số nguyên nên \(x-2\inƯ\left(17\right)=\left\{-17,-1,1,17\right\}\)
\(\Leftrightarrow x\in\left\{-15,1,3,19\right\}\).
Bài 2, 3, 4: Tương tự.