
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



cho mk hỏi ai chs lazi điểm danh cái đê ~ mk hỏi thật đấy k đùa nha ~ bình luận thì mk k cho 3 cái ~

1)
\(\hept{\begin{cases}\left(\sqrt{2}+\sqrt{3}\right)x-y\sqrt{2}=\sqrt{2}\\\left(\sqrt{2}+\sqrt{3}\right)x+y\sqrt{3}=-\sqrt{3}\end{cases}\Leftrightarrow\hept{\begin{cases}-y\left(\sqrt{2}+\sqrt{3}\right)=\sqrt{2}+\sqrt{3}\\\left(\sqrt{2}+\sqrt{3}\right)x+y\sqrt{3}=-\sqrt{3}\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}x=0\\y=-1\end{cases}}\)

4 \(x\sqrt{y-1}=\sqrt{x}\sqrt{xy-x}\le\frac{xy}{2}\)
5. cosi 1+x^2>=2x
=>(1+x^2)^2>=4x^2
1+1/y^4>=2/y^2
=>8>=8x^2/y^2
=>y^2>=x^2
cm tt => x^2>=y^2
c10 \(\sqrt{x^2-y^2-2x-2y}=\sqrt{\left(x-y\right)\left(x+y-2\right)}\le x-1\)
c13 pt 2 vô n
Đề giống sai quá. Đã cho hệ mà còn cho 2 ẩn độc lập với nhau vậy. Nếu độc lập vậy thì cho phương trình chứ cho hệ làm chi

\(\hept{\begin{cases}x^3-8x=y^3+2y\\x^2-3y^2=6\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}6\left(x^3-y^3\right)=6\left(8x+2y\right)\\x^2-3y^2=6\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}6\left(x^3-y^3\right)=\left(x^2-3y^2\right)\left(8x+2y\right)\\x^2-3y^2=6\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}24xy^2-2x^2y-2x^3=0\\x^2-3y^2=6\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x\left(3y-x\right)\left(4y+x\right)=0\\x^2-3y^2=6\end{cases}}\)
Đơn giản rồi làm tiếp nhé
\(\hept{\begin{cases}5x^2-3y=x-3xy\\x^3-x^2=y^2-3y^3\end{cases}}\)
Với x = 0 thì y = 0
Với x \(\ne\)0 thì nhân pt trên cho x ta được
\(\Leftrightarrow\hept{\begin{cases}5x^3-3yx=x^2-3x^2y\left(1\right)\\x^3-x^2=y^2-3y^3\left(2\right)\end{cases}}\)
Lấy (1) + (2) vế theo vế được
\(\Leftrightarrow6x^3-3xy-x^2=x^2+y^2-3x^2y-3y^3\)
\(\Leftrightarrow6x^3-3xy-2x^2-y^2+3x^2y+3y^3=0\)
\(\Leftrightarrow\left(x+y\right)\left(3y^2-3xy-y+6x^2-2x\right)=0\)
Tới đây thì đơn giản roofin làm tiếp nhé

Trừ vế ta có \(x^3-y^3+3\left(x-y\right)=8\left(y-x\right)\)
\(\Leftrightarrow\left(x-y\right)\left(x^2+xy+y^2\right)+3\left(x-y\right)+8\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x^2+y^2+xy+11\right)=0\)
Vì \(x^2+y^2+xy+11>0\forall x,y\)
=> x=y
Thay vào pt (1) giải nốt là ok nha bn !
_Kudo_

c) Ta có: \(\left\{{}\begin{matrix}\dfrac{x+2}{x+1}+\dfrac{2}{y-2}=6\\\dfrac{5}{x+1}-\dfrac{1}{y-2}=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x+1}+\dfrac{2}{y-2}=5\\\dfrac{5}{x+1}-\dfrac{1}{y-2}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{x+1}+\dfrac{10}{y-2}=25\\\dfrac{5}{x+1}-\dfrac{1}{y-2}=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{11}{y-2}=22\\\dfrac{1}{x+1}+\dfrac{2}{y-2}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y-2=\dfrac{1}{2}\\\dfrac{1}{x+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+1=1\\y-2=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\dfrac{5}{2}\end{matrix}\right.\)

\(\hept{\begin{cases}x-y=3\\3x-4y=2\end{cases}}\)
\(\hept{\begin{cases}x=y+3\\3x-4y=2\end{cases}}\)
\(\hept{\begin{cases}x=y+3\\3y+9-4y=2\end{cases}}\)
\(\hept{\begin{cases}x=y+3\\y=7\end{cases}}\)
\(\hept{\begin{cases}x=10\left(tm\right)\\y=7\left(tm\right)\end{cases}}\)
Vậy (x;y)=(10;7)
\(\hept{\begin{cases}\frac{x}{2}-\frac{y}{3}=1\\5x-8y=3\end{cases}}\)
\(\hept{\begin{cases}x-\frac{2y}{3}=2\\5x-8y=3\end{cases}}\)
\(\hept{\begin{cases}x=\frac{2y}{3}+2\\10+\frac{10y}{3}-8y=3\end{cases}}\)(thay x =2y/3 + 2 vào bthuc bên cạnh )
\(\hept{\begin{cases}x=2+\frac{2}{3}y\\-\frac{14}{3}y=-7\end{cases}}\)
\(\hept{\begin{cases}x=2+\frac{2}{3}\cdot\frac{3}{2}=3\\y=\frac{3}{2}\end{cases}}\)
Vậy (x;y)=(3:3/2)
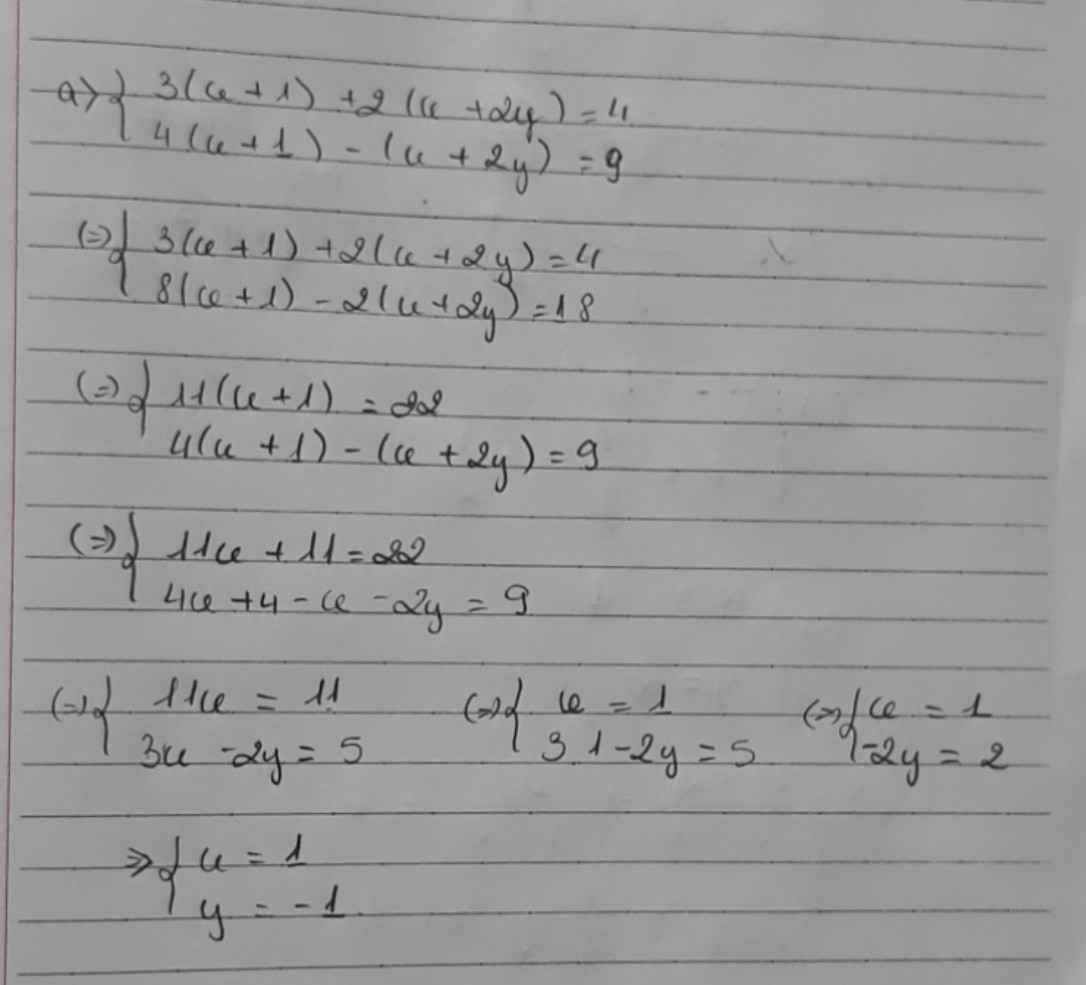
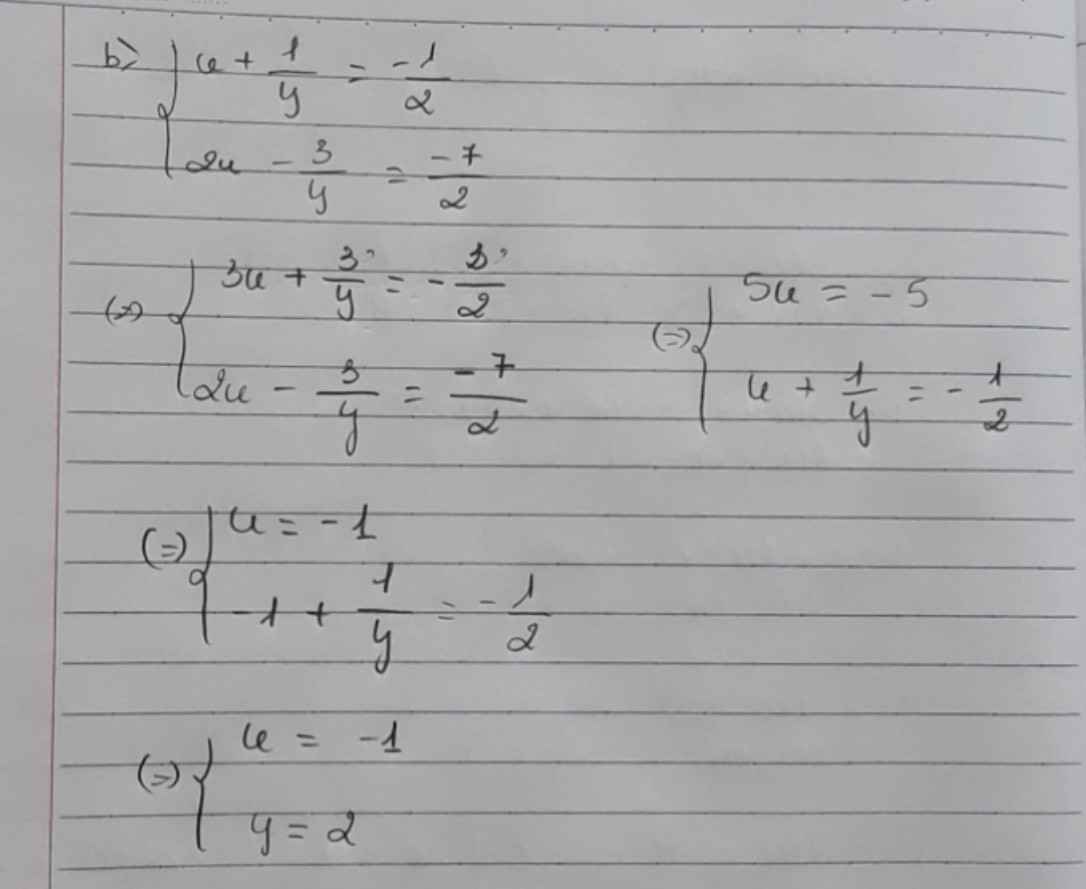
\(\hept{\begin{cases}5x+3y=2\\15x+8y=3\end{cases}}\)
\(< =>\hept{\begin{cases}15x+9y=6\\15x+8y=3\end{cases}}\)
\(< =>\hept{\begin{cases}x=6-3=3\\5x+3y=2\end{cases}}\)
\(< =>\hept{\begin{cases}x=3\\15+3y=2\end{cases}}\)
\(< =>\hept{\begin{cases}x=3\\y=-\frac{13}{3}\end{cases}}\)
ngáo rồi :(((
Dòng 2 \(< =>\hept{\begin{cases}y=3\\5x+3y=2\end{cases}}\)
\(< =>\hept{\begin{cases}y=3\\5x=-7\end{cases}< =>\hept{\begin{cases}x=-\frac{7}{5}\\y=3\end{cases}}}\)