Đáp án B

Có duy nhất mặt phẳng (SAC)

Chọn C.

Đáp án D

Hình hộp chữ nhật có 3 kích thước đôi một khác nhau có 3 mặt phẳng đối xứng đó là 3 mặt phẳng trung trực của các cạnh đáy và cạnh bên

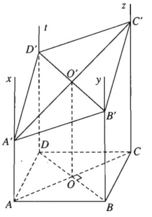
a) Ta có hai mặt phẳng song song là: (Ax, AD) // (By, BC)

Hai mặt phẳng này bị cắt bởi mặt phẳng (β) nên ta suy ra các giao tuyến của chúng phải song song nghĩa là A′D′ // B′C′.

Tương tự ta chứng minh được A′B′ // D′C′. Vậy A', B', C', D' là hình bình hành. Các hình thang AA'C'C và BB'D'D đều có OO' là đường trung bình trong đó O là tâm của hình vuông ABCD và O' là tâm của hình bình hành A',B',C',D'. Do đó: AA′ + CC′ = BB′ + DD′ = 2OO′

b) Muốn hình bình hành A',B',C',D' là hình thoi ta cần phải có A'C' ⊥ B'D'. Ta đã có AC ⊥ BD. Người ta chứng minh được rằng hình chiếu vuông góc của một góc vuông là một góc vuông khi và chỉ khi góc vuông đem chiếu có ít nhất một cạnh song song với mặt phẳng chiếu hay nằm trong mặt chiếu. Vậy A', B', C', D' là hình thoi khi và chỉ khi A'C' hoặc B'D' song song với mặt phẳng (α) cho trước. Khi đó ta có AA' = CC' hoặc BB' = DD'.

c) Muốn hình bình hành A', B', C', D' là hình chữ nhật ta cần có A'B' ⊥ B'C', nghĩa là A'B' hoặc B'C' phải song song với mặt phẳng (α)(α). Khi đó ta có AA' = BB' hoặc BB' = CC', nghĩa là hình bình hành A', B', C', D' có hai đỉnh kề nhau cách đều mặt phẳng (α) cho trước.

Chọn C

Đáp án D

Tồn tại 5 mặt phẳng thỏa mãn đề bài là:

-        Mp đi qua trung điểm AD,BC,SC,SD

-        Mp đi qua trung điểm CD,AB,SC,SB

-        Mp đi qua trung điểm AD,BC,SB,SA

-        Mp đi qua trung điểm CD,AB,SA,SD

-        Mp đi qua trung điểm SA,SB,SC,SD

Đáp án B

Gọi M,N,P,Q là trung điểm của AB,BC,CD,DA .

M’,N’,P’,Q’ là trung điểm của A’B’,B’C’,C’D’,D’A’.

R,K,H,I là trung điểm của AA’,BB’ ;CC’, DD’.

Hình lập phương gồm có 9 mặt phẳng đối xứng :

  (QNN’Q’),    (MPP’M’),    (RKHI)

  (ABC’D’),    (DCB’A’),    (BCD’A’),    

(ADC’B’),      (ACC’A’),    (BDD’B’)