Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ta có: BC = 1/2AD
SABC = SBCD
+ hai tam giác có chung đáy
+ có chiều cao bằng chiều cao hình thang
- mà 2 tam giác có chung SICB
=> cặp tam giác bằng nhau được tạo trong hình thang là SABI = SICD
b) BI = 1/3ID => SICB = 1/3SICD do 2 tam giác có chung cao hạ từ C xuống AB và đáy BI = 1/3IB
chứng minh ngược: SBCD = 1/3SABD vì 2 tam giác có chung chiều cao là chiều cao của hình thang
đáy BC = 1/3AD
mặt khác: 2 tam giác có chung đáy BD nên IC = 1/3AI
=> SAIB = 3SBIC
vì 2 tam giác có chung đường cao hạ từ B xuống AC
IC = 1/3AI
=> SAIB = 2/3SABC = 1/4.2/3(SABCD) = 2/12SABCD
=> 2/12SABCD = 2/12.48 = 8 cm^2
nguồn: Dũng Lê Trí

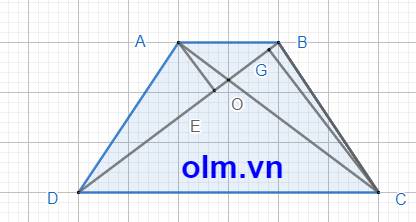
a, Dựng chiều cao CG của \(\Delta\)BCD và chiều cao AE của \(\Delta\) ABD
\(\dfrac{S_{ABD}}{S_{BCD}}\) = \(\dfrac{AE}{CG}\) (vì hai tam giác có chung cạnh đáy BD nên tỉ số diện tích là tỉ số hai chiều cao tương ứng)
\(\dfrac{S_{ABD}}{S_{BCD}}\) = \(\dfrac{AB}{CD}\) (vì hai tam giác có chiều cao bằng nhau nên tỉ số diện tích hai tam giác là tỉ số hai cạnh đáy)
⇒ \(\dfrac{AE}{CG}\) = \(\dfrac{AB}{CD}\) = \(\dfrac{1}{3}\)
\(\dfrac{S_{AOB}}{S_{BOC}}\) = \(\dfrac{AE}{CG}\) ( hai tam giác có chung cạnh đáy OB nên tỉ số diện tích là tỉ số hai chiều cao tương ứng)
\(\dfrac{S_{AOB}}{S_{BOC}}\) = \(\dfrac{AO}{OC}\) ( vì hai tam giác có chiều cao bằng nhau nên tỉ số diện tích là tỉ số hai cạnh đáy)
⇒ \(\dfrac{AE}{CG}\) = \(\dfrac{AO}{OC}\) = \(\dfrac{1}{3}\)
Chứng minh tương tự ta có: \(\dfrac{BO}{OD}\) = \(\dfrac{1}{3}\)
b, SABD = SABC ( vì hai tam giác có chung cạnh đáy AB và hai chiều cao bằng nhau)
SABD = SABO + SAOD = SAOB + SBOC = SABC
SAOD \(\times\) 1 = SBOC
SAOD \(\times\) 1 = SAOD
SAOD \(\times\) \(\dfrac{1}{3}\) = SAOB (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BD và \(\dfrac{OB}{OD}\) = \(\dfrac{1}{3}\))
SAOD \(\times\) 3 = SDOC ( vì hai tam giác có chung chiều cao hạ từ đỉnh D xuống đáy AC và \(\dfrac{AO}{OC}\) =\(\dfrac{1}{3}\))
Cộng các vế trên ta với nhau ta có diện tích hình thang ABCD bằng:
1 + 1 + \(\dfrac{1}{3}\) + 3 = \(\dfrac{16}{3}\) ( diện tích hình tam giác AOD)
Diện tích tam giác AOD là: 32 : \(\dfrac{16}{3}\) = 6 (m2)
ĐS...
Mọi ng giải nhanh giúp mình nhé, mình đag cần gấp lắm, mai đi học r, cảm ơn mng nh🥹

· a)Từ hình vẽ ta thấy diện tích tam giác ABC bằng diện tích tam giác BCD vì hai tam giác này chung đáy BC, khoảng cách từ A xuống BC bằng khoảng cách từ D xuống BC.
· Hai tam giác ABC và BCD có diện tích bằng nhau, hai tam giác này chung phần diện tích tam giác BIC nên phần diện tích còn lại của hai tam giác này cũng bằng nhau hay diện tích tam giác AIB bằng diện tích tam giác CID
· Vậy diện tích tam giác AIB bằng diện tích tam giác CID
· b)Diện tích tam giác BCD bằng 1313 diện tích tam giác ABD vì hai tam giác có chiều cao bằng nhau( cùng bằng chiều cao hình thang ) và đáy BC bằng 1313 đáy AD. Do đó diện tích tam giác ABC bằng diện tích tam giác BCD và bằng 1414 diện tích hình thang ABCD
· Diện tích tam giác ABC bằng diện tích tam giác BCD và bằng :
· 48:4=1248:4=12 (cm2��2 )
· Vì diện tích tam giác BCD bằng 1313 diện tích tam giác ABD, hai tam giác này chung đáy BD nên khoảng cách từ C đến BD bằng 1313 khoảng cách từ A xuống BD
· Diện tích tam giác AIB gấp 3 lần diện tích tam giác BIC vì hai tam giác này chung đáy BI và khoảng cách từ A đến BI gấp 3 lần khoảng cách từ C xuống BI. Do đó diện tích tam giác AIB bằng 3434 diện tích tam giác ABC
· Diện tích tam giác AIB là:
· 12:4×3=912:4×3=9 (cm2��2 )
· Đáp số 99 cm2��2
·

\(BC=\frac{1}{3}AD\)
\(S_{ABC}=S_{BCD}\)
- Hai tam giác có chung đáy
- Có chiều cao bằng chiều cao hình thang
+ Mặt khác :Hai tam giác có chung diện tích ICB nên từ đó suy ra :
Cặp tam giác bằng nhau tạo thành trong hình thang là :
\(S_{ABI}=S_{ICD}\)
b) \(S_{ABC}=\frac{1}{3}S_{ACD}\)
- Đáy BC = 1/3 đáy CD
- Có chiều cao bằng chiều cao hình thang
+ Vì hai tam giác có chung đáy AC nên chiều cao hạ từ B xuống I = 1/3 chiều cao hạ từ D xuống I
\(BI=\frac{1}{3}ID\)
Từ dữ kiện BI = 1/3 ID là bạn có thể tự chứng minh tiếp được rồi