Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét hình thang ABCD có
\(\widehat{C}=\widehat{D}=80^o\) => ABCD là hình thang cân => AD=BC
\(\Rightarrow\widehat{A}=180^o-\widehat{D}=180^o-80^o=100^o\) (Hai góc trong cùng phía)
Tương tự ta cũng có \(\widehat{B}=100^o\)
\(\Rightarrow\widehat{A}=\widehat{B}=100^o\)
Xét tg ABC và tg ABD có
AD=BC (cmt)
\(\widehat{A}=\widehat{B}\) (cmt)
AB chung
=> tg ABD = tg ABC (c.g.c) \(\Rightarrow\widehat{ADB}=\widehat{ACB}\)
Mà \(\widehat{ADB}+\widehat{BDC}=\widehat{ADC}=180^o=\widehat{BCD}=\widehat{ACB}+\widehat{ACD}\)
\(\Rightarrow\widehat{BDC}=\widehat{ACD}=\left(180^o-\widehat{CID}\right):2=60^o\)
=> tg CID là tg đều => CD=CI (1)
Xét tg ABI có
\(\widehat{BAC}=\widehat{ACD}=60^o\) (góc so le trong)
\(\widehat{ABD}=\widehat{BDC}=60^o\) (góc so le trong)
\(\widehat{AIB}=\widehat{CID}=60^o\) (góc đối đỉnh)
=> tg ABI là tg đều
Ta có AE là phân giác \(\widehat{BAI}\) (gt)
=> AE là đường trung trực, đường cao của tg ABI (trong tg đều đường phân giác đồng thời là đường cao, đường trung trực)
Xét tg BIE có
AE đồng thời là đường cao và đường trung trực => tg BIE cân tại E
\(\Rightarrow\widehat{DBC}=\widehat{BIE}\) (góc ở đáy tg cân)
Ta có
\(\widehat{DBC}=\widehat{B}-\widehat{ABD}=100^o-60^o=40^o=\widehat{BIE}\)
=> \(\widehat{BEI}=180^o-\left(\widehat{DBC}+\widehat{BIE}\right)=180^o-\left(40^o+40^o\right)=100^o\)
\(\Rightarrow\widehat{IEC}=180^o-\widehat{BEI}=180^o-100^o=80^o\)
Ta có
\(\widehat{BIC}=180^o-\widehat{CID}=180^o-60^o=120^o\)
\(\Rightarrow\widehat{EIC}=\widehat{BIC}-\widehat{BIE}=120^o-40^o=80^o\)
Xét tg CIE có
\(\widehat{IEC}=\widehat{EIC}=80^o\) => tg CIE cân tại C => CE=CI (2)
Từ (1) và (2) => CE=CD

a) Ta có:
\(\widehat{A}+\widehat{ABC}+\widehat{BCA}=180\)
\(\Rightarrow\widehat{BCA}=180-90-60=30\)
Vì \(BC\perp Cy\Rightarrow\widehat{BCy}=90\)
Mà \(\widehat{BCy}+\widehat{ECF}+\widehat{BCA}=180\)
\(\Rightarrow\widehat{ECF}=180-90-30=60\left(1\right)\)
Vì \(\widehat{FBC}+\widehat{BCA}+\widehat{BFC}=180\)
\(\Rightarrow\widehat{BFC}=180-\frac{\widehat{ABC}}{2}-\widehat{BCA}\)
\(\Rightarrow\widehat{BFC}=60\left(2\right)\)
Từ \(\left(1\right)\)và\(\left(2\right)\)\(\Rightarrow\Delta CEF\)là tam giác đều
a) Xét ΔABC∆ABC vuông tại AA
ˆABC=60oABC^=60o
⇒ACB=30o⇒ACB=30o
Ta có: BEBE là phân giác của ˆBB^
⇒ˆCBE=12ˆABC=30o⇒CBE^=12ABC^=30o
⇒ˆFEC=ˆECB+ˆEBC=60o⇒FEC^=ECB^+EBC^=60o
Xét ΔCBF∆CBF vuông tại CC có:
ˆCBF=30oCBF^=30o
⇒ˆCFB=60o⇒CFB^=60o
Xét ΔCEF∆CEF có:
ˆFEC=ˆCFB=60oFEC^=CFB^=60o
Do đó ΔCEG∆CEG đều
b) Sửa đề: ABCDABCD là hình thang cân
Ta có:
ˆBAC=ˆBDC=90oBAC^=BDC^=90o
Do đó ABCDABCD là tứ giác nội tiếp
⇒ˆACB=ˆADB=30o⇒ACB^=ADB^=30o
Ta lại có: ˆDBC=ˆACB=30oDBC^=ACB^=30o
nên ˆABD=ˆDBCABD^=DBC^
⇒ABCD⇒ABCD là hình thang đáy AB,CDAB,CD
Mặt khác: ΔDBC∆DBC vuông tại DD có:
ˆDBC=30oDBC^=30o
⇒ˆDCB=60o=ˆABC⇒DCB^=60o=ABC^
Do đó ABCDABCD là hình thang cân

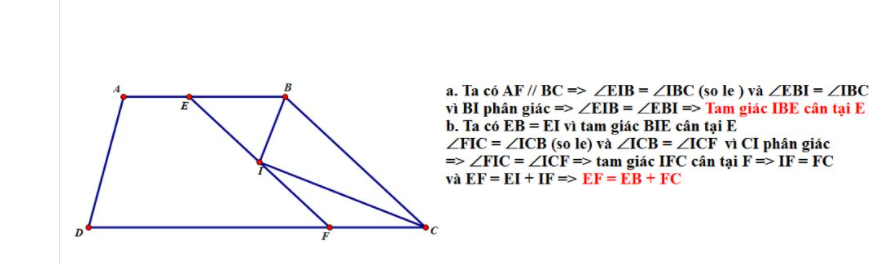
\(a,\) Ta có \(\widehat{B_1}=\widehat{B_2}\left(t/c.phân.giác\right);\widehat{B_2}=\widehat{I_1}\left(so.le.trong.do.EI//BC\right)\)
\(\Rightarrow\widehat{B_1}=\widehat{I_1}\Rightarrow\Delta BEI.cân.tại.E\)
Ta có \(\widehat{C_1}=\widehat{C_2}\left(t/c.phân.giác\right);\widehat{C_2}=\widehat{I_2}\left(so.le.trong.do.FI//BC\right)\)
\(\Rightarrow\widehat{C_1}=\widehat{I_1}\Rightarrow\Delta CFI.cân.tại.F\)
\(b,\) Vì \(\Delta BEI.và.\Delta CFI\) cân nên \(\left\{{}\begin{matrix}BE=EI\\CF=FI\end{matrix}\right.\)
\(\Rightarrow BE+CF=EI+FI=EF\)
Các hình thang: BEFC do EF//BC; ADFE do AE//DF; ABCD do giả thiết

Bài 1:
a.
AB // CD
=> A + D = 1800 (2 góc trong cùng phía)
=> A = 1800 - D = 1800 - 540 = 1260
AB // CD
=> B + C = 1800 (2 góc trong cùng phía)
=> B = 1800 - C = 1800 - 1050 = 750
b.
AB // CD
=> A + D = 1800 (2 góc trong cùng phía)
=> A = (1800 - 320) : 2 = 740
=> D = 1800 - 740 = 1060
AB // CD
=> B + C = 1800 (2 góc trong cùng phía)
=> B = 1800 : (1 + 2) . 2 = 1200
=> C = 1800 - 1200 = 600
Bài 2:
a: Xét ΔABE và ΔACF có
góc ABE=góc ACF
AB=AC
góc A chung
Do đó: ΔABE=ΔACF
Suy ra: AE=AF
b: Xét ΔABC có AF/AB=AE/AC
nên FE//BC
=>BFEC là hình thang
mà CF=BE
nên BFEC là hình thang cân
c: Xét ΔFEB có góc FEB=góc FBE
nên ΔFEB cân tại F
=>FE=FB=EC