Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
( hình tự vẽ)
a) xét tam giác AMO và tam giác AQO:
AO: cạnh chung
DAO = BAO
=> tam giác AQO= tam giác AMO ( ch-gn)
=> OM = OQ(1)
cm tương tự, xét tam giác MOB và tam giác NOB, tam giác QOD và tam giác POD.
=> OM=ON=OP=OQ
b) Ta có : OM vuông góc BA
OP vuông góc DC
Mà : AB//DC (ABCD là hình thoi )
=> M,O,P thẳng hàng
có thể cm rằng AMCP là hình bình hành cũng được
c) Ta có OM=ON=OP=OQ
M,O,P thẳng hàng (cmt)
Q,O,N thẳng hàng ( tự cm như cách trên )
=> MNPQ là hình chữ nhật
d) Ta có AQ=AM ( tam giác AQO=tam giác AMO)
Mà QAM =90* ( ABCD laqf hình vuông)
=> AQM =45*
AQM +OQM = 90*
=>OQM = 45*
Mà OQ=OM (cmt)
=> QOM = 90*
Mà MNPQ là hcn
=> MNPQ là hình vuông
- a)xét tg MOQ và tg NOP có: -góc Ở chung; OM=ON(giả thiết);OQ=OP(giả thiết)=>tg MOQ=tgNOP(cạnh.góc cạnh)
- b) ta có:QP (cạnh chung);MQ=NP(giả thiết);góc M=góc N(tg MOQ=tgNOP)=>tg MPQ=tg NQP
- c) MN//PQ( vị trí so le trong)
d) vì MN//PQ(cmt)=>MNPQ là ht cân
Ta có: MN // AB (gt); AB // CD(gt) => MN // AB // CD
Xét tam giác ABC có: OM // AB (MN // AB)
=> \(\dfrac{OM}{AB}=\dfrac{CM}{CA}\) (hệ quả định lý Ta lét trong tam giác) (1)
Xét tam giác ABD có: ON // AB (MN // AB)
=> \(\dfrac{ON}{AB}=\dfrac{DN}{DB}\) (hệ quả định lý Ta lét trong tam giác) (2)
Xét hình thang ABCD có: MN // AB // CD (cmt)
=> \(\dfrac{CM}{CA}=\dfrac{DN}{DB}\) (định lý Ta lét trong hình thang) (3)
Từ (1) (2) (3) => OM = ON
Trong ΔDAB, ta có: OM // AB (gt)
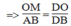(Hệ quả định lí Ta-lét) (1)
Trong ΔCAB, ta có: ON // AB (gt)
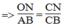(Hệ quả định lí Ta-lét) (2)
Trong ΔBCD, ta có: ON // CD (gt)
Suy ra: 
(định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra: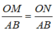 
Vậy: OM = ON
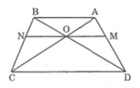
Xét ΔMNQ và ΔNMP có
MN chung
NQ=MP
MQ=NP
=>ΔMNQ=ΔNMP
=>góc OMN=góc ONM
=>OM=ON
OM+OP=MP
ON+OQ=NQ
mà MP=NQ và OM=ON
nên OP=OQ