Xét ΔABD có AB=AD và góc A=60 độ

=>ΔABD đều

=>góc ABD=góc ADB=60 độ và AB=AD=BD

Xét ΔBCD có CB=CD và góc C=60 độ

nên ΔBCD đều

=>BD=CB=CD và góc CBD=góc CDB=60 độ

Xét ΔBAM và ΔBDN có

BA=BD

góc BAM=góc BDN

AM=DN

=>ΔBAM=ΔBDN

=>BM=BN và góc ABM=góc DBN

=>góc DBN+góc DBM=60 độ

=>góc MBN=60 độ

=>ΔMBN đều

https://tailieumoi.vn/cau-hoi/hinh-thoi-abcd-co-goc-a-60-do-tren-canh-ad-lay-diem-m-tren-canh-137282.html

Nhắc lần thứ nhất, không copy câu trả lời từ nguồn khác.

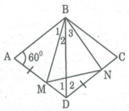
Nối BD, ta có AB = AD (gt)

Suy ra ∆ ABD cân tại A

Mà ∠ A = 60 0  ⇒  ∆ ABD đều

⇒  ∠ (ABD) =  ∠ D 1 =  60 0  và BD = AB

Suy ra: BD = BC = CD

⇒ ∆ CBD đều ⇒  ∠ D 2 =  60 0

Xét  ∆ BAM và  ∆ BDN,ta có:

AB = BD ( chứng minh trên)

∠ A =  ∠ D 2  =  60 0

AM = DN (giả thiết)

Do đó  ∆ BAM =  ∆ BDN ( c.g.c) ⇒  ∠ B 1 =  ∠ B 3  và BM = BN

Suy ra ΔBMN cân tại B.

Mà  ∠ B 2 + ∠ B 1  =  ∠ (ABD) =  60 0

Suy ra:  ∠ B 2 +  ∠ B 3  =  ∠ B 2  +  ∠ B 1  = 60° hay  ∠ (MBN) =  60 0

Vậy  ∆ BMN đều

1:

Vì AE=CF và AE//CF (AB//CD do hbh ABCD) nên AECF là hbh

\(\left\{{}\begin{matrix}AE=CF\\AM=CN\\\widehat{A}=\widehat{C}\left(hbh.ABCD\right)\end{matrix}\right.\Rightarrow\Delta AME=\Delta CNF\left(c.g.c\right)\\ \Rightarrow ME=NF\left(4\right)\\ \left\{{}\begin{matrix}AE=CF\\AB=CD\end{matrix}\right.\Rightarrow AB-AE=CD-CF\Rightarrow BE=DF\left(1\right)\\ \left\{{}\begin{matrix}AM=CN\\AD=BC\end{matrix}\right.\Rightarrow AD-AM=CN-BC\Rightarrow DM=BN\left(2\right)\)

ABCD là hbh nên \(\widehat{B}=\widehat{D}\left(3\right)\)

\(\left(1\right)\left(2\right)\left(3\right)\Rightarrow\Delta DMN=\Delta BFE\left(c.g.c\right)\\ \Rightarrow MN=EF\left(5\right)\)

(4)(5) suy ra MENF là hbh