Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(=>vtb2=\dfrac{v2+v3}{2}=\dfrac{18+12}{2}=15km/h\)
\(=>vtb=\dfrac{S}{\dfrac{\dfrac{1}{2}S}{v1}+\dfrac{\dfrac{1}{2}S}{vtb2}}=\dfrac{S}{\dfrac{S}{50}+\dfrac{S}{30}}=\dfrac{S}{\dfrac{80S}{1500}}=\dfrac{1500}{80}=18,75km/h\)

thời gian đi nửa quãng đầu \(t_1=\dfrac{1}{2}S.\dfrac{1}{25}=\dfrac{S}{50}\)
nửa quãng sau \(\dfrac{1}{2}t_2.18+\dfrac{1}{2}t_2.12=\dfrac{1}{2}S\Leftrightarrow t_2=\dfrac{S}{30}\)
vận tốc trung bình \(v_{tb}=\dfrac{S}{t_1+t_2}=\dfrac{S}{S.\left(\dfrac{1}{50}+\dfrac{1}{30}\right)}=\dfrac{1}{\dfrac{1}{50}+\dfrac{1}{30}}=18,75\left(km/h\right)\)

Nửa quãng đường đầu của đoạn AB là :
\(s_1=\dfrac{s}{2}=v_1.t=25t\left(km\right)\) \(\left(1\right)\)
Quãng đường vật đó đi trong nửa thời gian đầu của đoạn đường sau là :
\(s_2=v_2.t_2=18t_2\left(km\right)\)
Quãng đường vật đó đi trong nửa thời gian sau của đoạn đường sau là :
\(s_3=v_3.t_2=12t_2\left(km\right)\)
Mà : \(s_2+s_3=\dfrac{s}{2}\)
\(\Leftrightarrow18t_2+12t_2=\dfrac{s}{2}\)
\(\Leftrightarrow30t_2=\dfrac{s}{2}\) \(\left(2\right)\)
Từ \(\left(1\right)+\left(2\right)\Leftrightarrow25t_1=30t_2\)
\(\Leftrightarrow1,2t_1=t_2\)
Vận tốc trung bình của vật đó trên cả đoạn đường AB là :
\(v_{tb}=\dfrac{s_1+s_2+s_3}{t_1+t_2}=\dfrac{2.25t_1}{t_1+1,2t_1}=22,3\left(km\backslash h\right)\)
Vậy...

Vận tốc trung bình là:
\(\dfrac{S_1+S_2+S_3}{t_1+t_2+t_3}=\dfrac{S}{t_1+t_4}\)(*)(t4 = t2 + t3)
thời gian nửa quãng đường đầu đi được là:
\(t1=\dfrac{S1}{v1}=\dfrac{S}{2.v1}=\dfrac{S}{2.25}=\dfrac{S}{50}\left(1\right)\)
Ta lại có:
\(S2+S3=\dfrac{S}{2}\Leftrightarrow v2.t2+t3.v3=\dfrac{S}{2}\)
\(\Leftrightarrow18.t2+12.t3=\dfrac{S}{2}\)
\(\Leftrightarrow\dfrac{18t_4}{2}+\dfrac{12t_4}{2}=\dfrac{S}{2}\)
\(\Leftrightarrow40t_4=S\)
\(\Rightarrow t_4=\dfrac{S}{40}\left(2\right)\)
Thay (1) và (2) vào (*) ta được:
\(v_{tb}=\dfrac{S}{\dfrac{S}{50}+\dfrac{S}{40}}=\dfrac{S}{S\left(\dfrac{1}{50}+\dfrac{1}{40}\right)}=\dfrac{1}{\dfrac{1}{50}+\dfrac{1}{40}}=\dfrac{200}{9}\approx22,\overline{2}\) (km/h)
Gọi 1/2 quãng đg là S km
Gọi thời gian đi đoạn đường đầu là t1 h
1/2 thời gian đi đoạn đường sau là t2 h
Trên đoạn đường đầu ta có; S=v1.t1=25t1(1)
Trên đoạn đường sau ta có: v2.t2+v3.t2=S
<=> (12+18) t2 =S
<=> 30.t2=S(2)
Từ (1) và (2) có; 30.t2=25.t1
<=>t2=1,2.t1
=>Vtb=\(\dfrac{2S}{t1+t2}\)=\(\dfrac{2.25.t1}{1,2t1+t1}\)=\(\dfrac{50}{2,2}\)\(\approx\)22,73(km/h)

*Trong nửa quãng đường còn lại:
S2 là quãng đường đi được trong 1/3 thời gian
S3 là quãng đường đi được trong 2/3 thời gian
t là thời gian đi được trong giai đoạn hai
Ta có:
Vtb= \(\dfrac{S_2+S_3}{t}\)
=\(\dfrac{V_2\times\dfrac{t}{3}+V_3\times\dfrac{2t}{3}}{t}\)
= \(\dfrac{\dfrac{17t}{3}+\dfrac{28t}{3}}{t}\)
=\(\dfrac{\dfrac{45t}{3}}{t}\)=\(\dfrac{15t}{t}\)= 15 (km/h)
* Trên cả quảng đường:
S1 là nửa quãng đường AB
t1 là thời gian đi trong 1/2 đoạn đường đầu
t2 là thời gian đi trong đoạn đường còn lại
Ta có:
Vtb'= \(\dfrac{2S_1}{t_1+t_2}\)= \(\dfrac{2S_1}{\dfrac{S_1}{V_1}+\dfrac{S_1}{V_{tb}}}\)= \(\dfrac{2}{\dfrac{1}{25}+\dfrac{1}{15}}\)=18,75 (km/h)
Vậy vận tốc trung bình trên cả quãng đường là 18,75 km/h

Cho đồ thị vận tốc – thời gian của một vật như hình dưới. Đoạn đồ thị nào biểu diễn vật chuyển động đều?
A. AB. B. BC. C. CD. D. BC và CD.
Bài giải:
Trên đoạn AB vận tốc là đường nằm ngang nên quãng đường AB vật chuyển động đều.
Chọn A
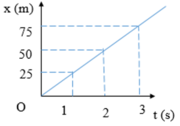
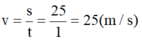

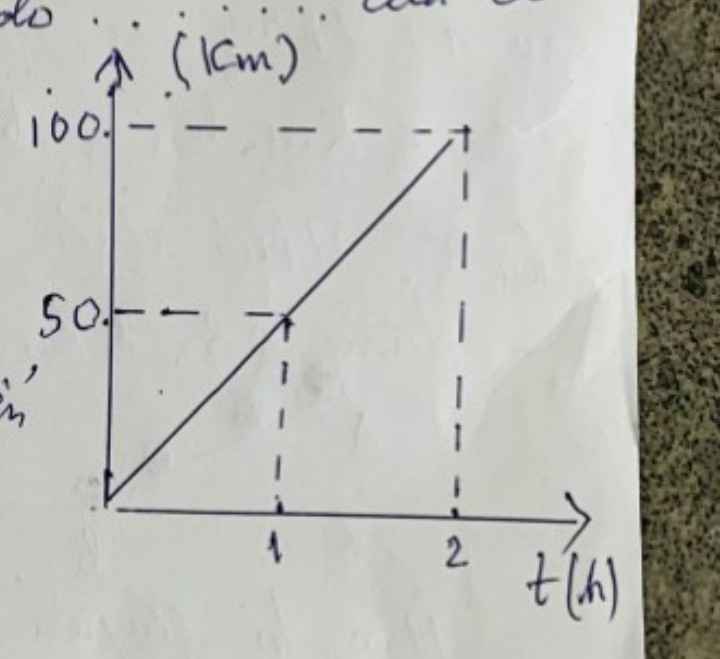 cho đồ thị diễn tả quãng đường đi của một chuyển động đều theo thời gian vận tốc của chuyển động đều này có độ lớn
cho đồ thị diễn tả quãng đường đi của một chuyển động đều theo thời gian vận tốc của chuyển động đều này có độ lớn
Đáp án B
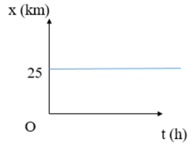
Dựa vào đồ thị ta thấy khoảng cách của vật với mốc không thay đổi theo thời gian. Như vậy vật luôn cách mốc 25km.