Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

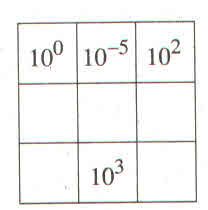
Tích của mỗi hàng, cột, đường chéo là:
100.10-5.102 = 10–3
Từ đó ta điền được vào các ô trống còn lại như sau:
| 100 | 10-5 | 102 |
| 101 | 10-1 | 10-3 |
| 10-4 | 103 | 10-2 |

Bài làm:
| \(2^7\) | \(2^0\) | \(2^5\) |
| \(2^2\) | \(2^4\) | \(2^6\) |
| \(2^3\) | \(2^8\) | \(2^1\) |

| 27 | 20 | 25 |
| 22 | 24 | 26 |
| 23 | 28 | 21 |
k tui k lại!LƯU Ý:NGƯỜI HƠN 10 ĐIỂM HỎI ĐÁP THÌ ĐƯỢC K!

bài này cũng khá khó gặm but đối với anh thì khác!
Vì bảng ô vuông có kích thước 5x5 nên có tất cả:5 hàng,5 cột,2 đường chéo nên có tất cả 12 tổng.
Do khi điền vào các ô là các số 0,1,-1 nên mỗi tổng(S) là một số nguyên thỏa mãn:\(-5\le S\le5\)
\(\Rightarrow\)có 11 giá trị trong khi đó có 12 tổng nên theo nguyên lý Đi-rích-lê(hay còn gọi là chuồng thỏ) thì tồn tại ít nhất 2 tổng có giá trị bằng nhau.
Bài toán được chứng minh_._
Vì bảng ô vuông có kích thước 5x5 nên có tất cả:5 hàng,5 cột,2 đường chéo nên có tất cả 12 tổng.
Do khi điền vào các ô là các số 0,1,-1 nên mỗi tổng(S) là một số nguyên thỏa mãn:−5≤S≤5
⇒có 11 giá trị trong khi đó có 12 tổng nên theo nguyên lý Đi-rích-lê(hay còn gọi là chuồng thỏ) thì tồn tại ít nhất 2 tổng có giá trị bằng nhau.
(ĐPCM)

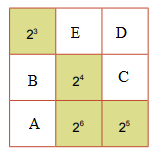
Ta đặt các ô chưa biết như sau:
Ta có:
Tích của mỗi hàng, cột, đường chéo bằng: \({2^3}{.2^4}{.2^5} = {2^{3 + 4 + 5}} = {2^{12}}\)
\(\begin{array}{l}A = {2^{12}}:{2^6}:{2^5} = {2^{12 - 6 - 5}} = {2^1} = 2;\\B = {2^{12}}:{2^1}:{2^3} = {2^{12 - 1 - 3}} = {2^8};\\C = {2^{12}}:{2^8}:{2^4} = {2^{12 - 8 - 4}} = {2^0} = 1;\\D = {2^{12}}:{2^0}:{2^5} = {2^{12 - 0 - 5}} = {2^7};\\E = {2^{12}}:{2^7}:{2^3} = {2^{12 - 7 - 3}} = {2^2}\end{array}\)
Vậy ta có bảng hoàn chỉnh là:

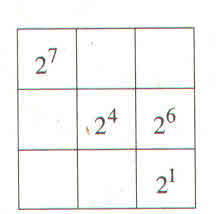

Tích của mỗi hàng, mỗi cột,mỗi đường chéo là:
27.24.21 = 27+ 4+ 1 = 212
Từ đó ta điền được vào các ô trống còn lại như sau: