Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn:
* Trường hợp 1: Quá trình cung cấp liên tục.
![]()
Tổng năng lượng cung cấp có ích sau thời gian t:
A c ó í c h = P c ó í c h . t = W ∆ t t
Tổng năng lượng cung cấp toàn phần sau thời gian t:
A t o à n p h ầ n = A c ó í c h H = 1 H W ∆ t 1
Mặt khác: A t p = E Q 2
Từ (1) và (2) suy ra:
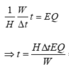
= 0 , 25 . 140 . 3 . 10000 0 , 049 s x 1 n g à y 86400 s ≈ 248 n g à y
* Trường hợp 2: Quá trình cung cấp chỉ diễn ra trong thời gian ngắn sau mỗi nửa chu kì thì năng lượng cần cung cấp sau mỗi nửa chu kì đúng bằng công của lực ma sát thực hiện trong nửa chu kì đó: ∆ W 1 / 2 = F m s . 2 A . Do đó, năng lượng có ích cần cung cấp:
A c ó í c h = ∆ W 1 / 2 x S ố n ử a c h u k ì = ∆ W 1 / 2 . t 0 , 5 T 1
Mặt khác:


Thay (2) vào (1): A c ó í c h = W ∆ t . T . t 0 , 5 T = 2 . W ∆ t t
Tổng năng lượng cung cấp toàn phần sau thời gian t: A t o à n p h ầ n = A c ó í c h H = 2 1 H . W ∆ t t
Mặt khác: A t o à n p h ầ n = E Q n ê n :

= 1 2 0 , 25 . 140 . 3 . 10000 0 , 049 s x 1 n g à y 86400 s ≈ 124 n g à y

Điện xoay chiều thú vị ở chỗ đó, chúng ta có thể dùng biến đổi đại số, dùng giản đồ véc tơ (tạm gọi là véc tơ thường - véc tơ buộc và véc tơ trượt), ngoài ra còn có thể dùng số phức để giải. Tùy từng bài toán và tùy từng kinh nghiệm của mỗi người thì sẽ biết nên làm theo cách nào cho hợp lí. Em hãy cứ làm nhiều bài tập điện xoay chiều thì em sẽ nhận ra điều đó.
Dùng giản đồ véc tơ thường thì hầu như dạng bài tập nào cũng giải được.
Còn véc tơ trượt là một biến thể của véc tơ thường (dựa vào tính chất cộng véc tơ trong toán học), làm cho hình vẽ đỡ rối hơn.
Còn nên dùng theo cách nào thì như mình nói tùy từng bài toán và kinh nghiệm của mỗi người. Kinh nghiệm của mình là những bài toán mà cho mối liên hệ các điện áp chéo nhau (VD: URL, URC,...) thì dùng véc tơ thường, trường hợp còn lại thì dùng véc tơ trượt.

Giả sử nguồn có công suất P,
S là diện tích của máy dò
Để máy dò còn dò được ánh sáng thí số lượng photon đến máy trong một đơn vị thời gian là n
Tại điểm cách xa r1
\(\frac{P}{4\pi r^2_1}.S=n.\frac{hc}{\lambda_1}\)
Tương tự ta có
\(\frac{P}{4\pi r^2_2}.S=n.\frac{hc}{\lambda_2}\)
Từ đó suy ra
\(\frac{r^2_1}{\lambda_1}=\frac{r^2_2}{\lambda_2}\)
\(\frac{r_1}{r_2}=\sqrt{\frac{\lambda_1}{\lambda_2}}=\frac{5}{6}\)
\(r_1=150km\)

Việc bắn và đo luân phiên nhằm mục đích loại trừ ảnh hưởng của gió.
Việc bắn đích và đo luân phiên nhằm mục tiêu xác định tốc độ âm thanh trong không khí. Bằng cách đo thời gian từ lúc thấy lửa loé ra súng súng đến lúc phát hiện tiếng nổ, ta có thể tính toán khoảng cách giữa hai nhà vật lý. Sau đó, dựa vào khoảng cách và thời gian, ta có thể tính tốc độ âm thanh trong không khí.

Gọi L là khoảng cách Trái Đất – Mặt Trăng: c = 3. 10 8 m/s là tốc độ ánh sáng; t là thời gian để ánh sáng đi về giữa Trái Đất và Mặt Trăng.
Ta có: 2L = ct.
![]()

