
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \({\left( {3x + y} \right)^4} = {\left( {3x} \right)^4} + 4.{\left( {3x} \right)^3}y + 6.{\left( {3x} \right)^2}{y^2} + 4.\left( {3x} \right){y^3} + {y^4}\)
\( = 81{x^4} + 108{x^3}y + 54{x^2}{y^2} + 12x{y^3} + {y^4}\)
b) \(\begin{array}{l}{\left( {x - \sqrt 2 } \right)^5} = \left( {x + (-\sqrt 2) } \right)^5 ={x^5} + 5.{x^4}.\left( { - \sqrt 2 } \right) + 10.{x^3}.{\left( { - \sqrt 2 } \right)^2} + 10.{x^2}.{\left( { - \sqrt 2 } \right)^3} + 5.x.{\left( { - \sqrt 2 } \right)^4} + 1.{\left( { - \sqrt 2 } \right)^5}\\ = {x^5} - 5\sqrt 2 .{x^4} + 20{x^3} - 20\sqrt 2 .{x^2} + 20x - 4\sqrt 2 \end{array}\)

SHTQ là: \(C^k_4\cdot\left(x^3\right)^{4-k}\cdot\left(\dfrac{1}{x}\right)^k=C^k_4\cdot x^{12-4k}\)
Số hạng ko chứa x tương ứng với 12-4k=0
=>k=3
=>SH đó là \(C^3_4=4\)

Ta có:
\({(2 + 3x)^4} = C_4^0{2^4} + C_4^1{2^3}3x + C_4^2{2^2}{\left( {3x} \right)^2} + C_4^32.{\left( {3x} \right)^3} + C_4^4{\left( {3x} \right)^4}\)
=> Hệ số của của \({x^2}\)là \(C_4^2{.2^2}{.3^2} = 36C_4^2.\)
Chọn D.

Ta có:
\({(2x + 3)^5} = 32{x^5} + 240{x^4} + 720{x^3} + 1080{x^2} + 810x + 243\)
Hệ số của \({x^3}\) là 720
Hệ số của \({x^4}\) là 240.
Vậy hệ số của \({x^3}\) lớn hơn hệ số của \({x^4}\).

SHTQ của \(\left(3x+2\right)^5\) là \(C^k_5\cdot\left(3x\right)^{5-k}\cdot2^k=C^k_5\cdot3^{5-k}\cdot2^k\cdot x^{5-k}\)
Hệ số của số hạng chứa x tương ứng với 5-k=1
=>k=4
=>Hệ số là \(C^4_5\cdot3^{5-4}\cdot2^4=240\)

Ta có:
\(A_n^2 + 24C_n^1 = \frac{{n!}}{{\left( {n - 2} \right)!}} + 24.\frac{{n!}}{{1!\left( {n - 1} \right)!}} = n(n - 1) + 24n\)
\( \Leftrightarrow {n^2} + 23n = 140 \Leftrightarrow \left[ \begin{array}{l}n = 5\\n = - 28\;(L)\end{array} \right.\)
Thay \(a = 2x,b = - 1\) trong công thức khai triển của \({(a + b)^5}\), ta được:
\(\begin{array}{l}{(2x - 1)^5} = {\left( {2x} \right)^5} + 5.{\left( {2x} \right)^4}.( - 1) + 10.{\left( {2x} \right)^3}.{( - 1)^2}\\ + 10.{\left( {2x} \right)^2}.{( - 1)^3} + 5.(2x).{( - 1)^4} + {( - 1)^5}\\ = 32{x^5} - 80{x^4} + 80{x^3} - 40{x^2} + 10x - 1\end{array}\)

\(\left(2x^2-\dfrac{1}{x^2}\right)^4=C^k_4\left(2x^2\right)^{4-k}\left(-\dfrac{1}{x^2}\right)^k\)
\(=C^k_4.2^{4-k}.x^{8-2k-2k}.\left(-1\right)^k\)
\(=C^k_4.2^{4-k}.x^{8-4k}.\left(-1\right)^k\)
\(ycbt\Leftrightarrow8-4k=0\Leftrightarrow k=2\)
\(\Rightarrow C^2_4.2^{4-2}.\left(-1\right)^2=24\)
Vậy số hạng không chứa \(x\) trong khai triển là \(24\).
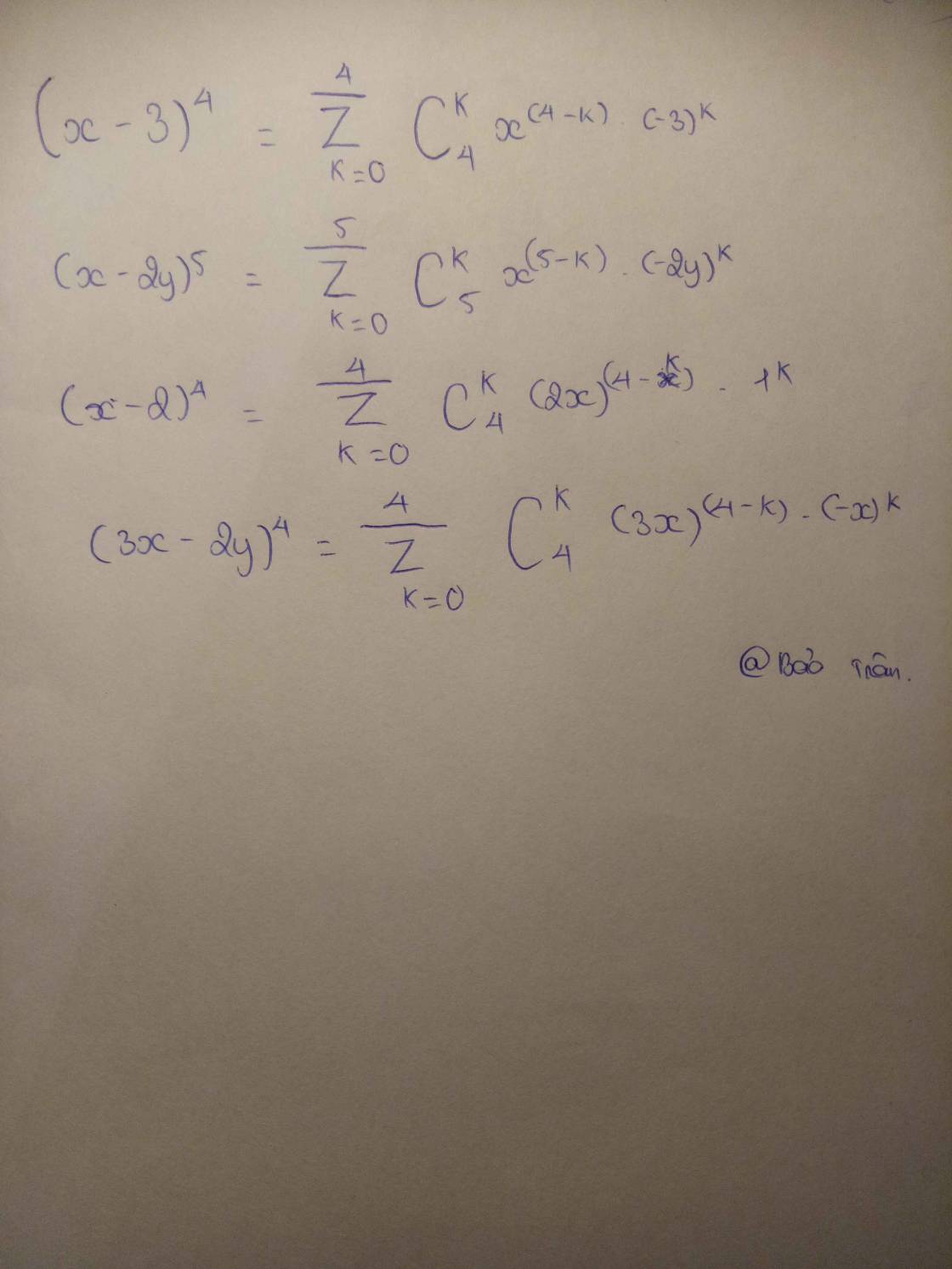
(x^2+1/x)^4
\(=C^0_4\cdot\left(x^2\right)^4+C^1_4\cdot\left(x^2\right)^3\cdot\left(\dfrac{1}{x}\right)+C^2_4\cdot\left(x^2\right)^2\cdot\left(\dfrac{1}{x}\right)^2+C^3_4\cdot\left(x^2\right)^1\cdot\left(\dfrac{1}{x}\right)^3+C^4_4\cdot\left(x^2\right)^0\cdot\left(\dfrac{1}{x}\right)^4\)
=x^8+4x^5+6x^3+4/x+1/x^4
cho hỏi là x ở\(\dfrac{1}{x}\) là nhân như n v