Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

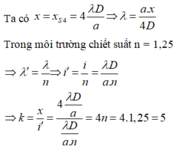
Vậy tại điểm M vân sáng bậc 4 chuyển thành vân sáng bậc 5.
Đáp án C

Bề rộng của 10 khoảng vân là 1,6 cm
=> \(10.i =1,6 cm=> i = 0,16 cm = 1,6mm.\)
\(\frac{x_A}{i}= 2,5 = 2+0,5\)=> A là vân tối thứ 3.
Em xin công thức với mà ct này dùng tính cái gì em đọc không hiểu

Chọn đáp án A
Gọi i và i’ lần lượt là khoảng vân khi thí nghiệm giao thoa thực hiện trong không khí và trong nước
⇒ M N = 10 i → M N 2 i ' = 10 i 2 i ' = 5. i i ' = 5 λ λ ' = 5 c / f v / f = 5 c v = 5 n = 5.4 / 3 = 6 , 67 ( λ , λ ' là bước sóng ánh sáng trong không khí và trong nước)
→ số vân sáng trên đoạn MN khi thí nghiệm giao thoa thực hiện trong nước là 2.6 + 1 = 13.

Gọi i và i’ lần lượt là khoảng vân khi thí nghiệm giao thoa thực hiện trong không khí và trong nước
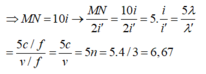
(λ, λ′ là bước sóng ánh sáng trong không khí và trong nước)
→ số vân sáng trên đoạn MN khi thí nghiệm giao thoa thực hiện trong nước là 2.6 + 1 = 13.
Đáp án C

Cách giải:
Giải: Trong không khí vị trí vân sáng bậc 2 là: b 1 = 2 λ D a ; khoảng vân c 1 = λ D a
số vân sáng quan sát được trên màn là:
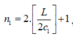
trong đó L là bề rộng trường giao thoa.
Làm thí nghiệm trên trong nước có chiết suất n > 1, với D,a và vị trí của S không đổi thì vị trí vân sáng bậc 2 là:
b
2
=
2
λ
D
n
a
; khoảng vân
c
1
=
λ
D
n
a
; số vân sáng quan sát được trên màn là:
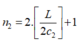
So sánh ta thấy: b1 > b2; c1 >c2; n1 < n2 => chọn B

Tại vân tối thứ k của 1 bức xạ nào đó có N vân sáng, ta có: \(x=(k+0,5)i=k'.i'\)(*)
Trong môi trường chiết suất n thì bước sóng, khoảng vân giảm đi n lần.
Khi đó, \(i=2i_1;i'=2i_1'\)
Thay vào (*) ta được: \(x=(2k+1)i_1=2k'i_1'\)(**)
Biểu thức (**) đều là điều kiện cho vân sáng.
Như vậy, ta sẽ có (N+1) vân sáng.

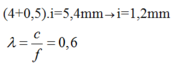
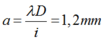
Chọn đáp án B
Ta có x = x S 4 = 4 λ D a ⇒ λ = a . x 4 D
Trong môi trường chiết suất n = 1,25
⇒ λ ' = λ n ⇒ i ' = i n = λ D a . n ⇒ k = x i ' = 4 λ D a λ D a . n = 4 n = 4.1 , 25 = 5
Vậy tại điểm M vân sáng bậc 4 chuyển thành vân sáng bậc 5