

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn D
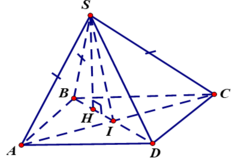
Gọi I là tâm hình thoi ABCD, H là hình chiếu của S lên mặt phẳng (ABCD).
Ta có SA = SB = SC nên hình chiếu vuông góc của S xuống mặt phẳng (ABCD) trùng với tâm đường tròn ngoại tiếp ΔABC hay H ∈ BI
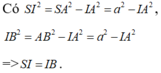
Khi đó tam giác SBD vuông tại S.
Hoặc ΔABC = ΔASC = ΔADC (c-c-c) nên IB = IS = ID, do đó ΔSBD vuông tại S.
Giả sử SD = x.
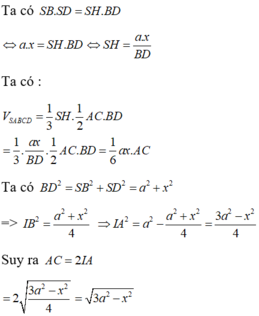
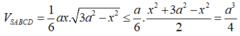

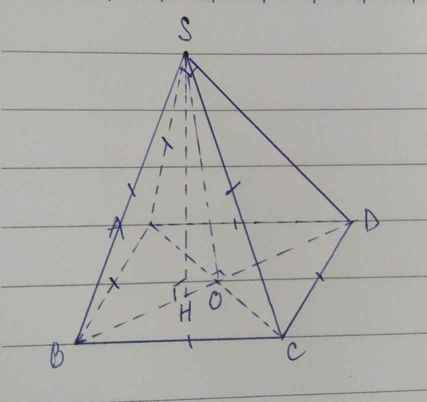
Gọi H là hình chiếu của S lên mp(ABCD), suy ra H thuộc BD (ABCD là hình thoi, SA=SB=SC).
Ta có: SA=SC=BA=BC=3 cm, suy ra SO=BO, suy ra tam giác SBD là tam giác vuông (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền).
0,5.SB.SD=6, suy ra SD=4 cm, suy ra BD=5 cm, AC=\(\sqrt{11}\) cm, SH=2,4 cm.
Thể tích cần tìm là V=1/3.2,4.0,5.5.\(\sqrt{11}\)=2\(\sqrt{11}\) (cm3).

Đáp án C
Gọi M, N lần lượt là trung điểm của AB và CD
Tam giác SAB cân tại S suy ra S M ⊥ A B
⇒ S M ⊥ d , với d = ( S A B ) ∩ ( S C D )
Vì ( S A B ) ⊥ ( S C D ) suy ra S M ⊥ ( S C D )
![]()
Kẻ S H ⊥ M N ⇒ S H ⊥ ( A B C D )
Ta có S ∆ S A B + S ∆ S C D = 7 a 2 10
![]()
⇒ S M + S N = 7 a 5
Tam giác SMN vuông tại S nên S M 2 + S N 2 = M N 2 = a 2
Giải hệ S M + S N = 7 a 5 S M 2 + S N 2 = a 2
![]()
![]()
Vậy thể tích khối chóp V S . A B C D = 1 3 . S A B C D . S H = 4 a 3 25