Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét hệ phương trình − x + 5 y = − 1 5 x + y = 2 có − 1 5 ≠ 5 1 nên hệ phương trình có nghiệm duy nhất
Đáp án: C

Xét hệ phương trình − 2 x + y = − 3 3 x − 2 y = 7 có − 2 3 ≠ 1 − 2 nên hệ phương trình có nghiệm duy nhất
Đáp án: C

Xét hệ phương trình 2 x − 2 y = 3 3 2 x − 6 y = 5 có 2 3 2 = − 2 − 6 ≠ 3 5 ⇔ 1 3 = 1 3 ≠ 3 5 nên hệ phương trình vô nghiệm
Đáp án: B

Đáp án C
Tập nghiệm phương trình -2x + y = -3 được biểu diễn bởi đường thẳng -2x + y = -3
Tập nghiệm phương trình 3x – 2y = 7 được biểu diễn bởi đường thẳng 3x – 2y = 7
Ta có 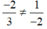 ⇒ phương trình có một nghiệm duy nhất
⇒ phương trình có một nghiệm duy nhất

Xét hpt \(\hept{\begin{cases}2x+y=3\left(a=2;b=1;c=3\right)\\3x-y=1\left(a'=3;b'=-1;c'=1\right)\end{cases}}\)
Ta có \(\frac{a}{a'}=\frac{2}{3}\)và \(\frac{b}{b'}=\frac{1}{-1}=-1\), do đó \(\frac{a}{a'}\ne\frac{b}{b'}\), dẫn đến hpt đã cho chỉ có 1 nghiệm duy nhất.
\(\Rightarrow\)Chọn A

6:
a: f(-2)=-1/2*(-2)^2=-2
=>Loại
b: f(4)=-1/2*4^2=-8=yB
=>B thuộc (P)
c: f(2)=-1/2*2^2=-2
=>Loại
5: f(-2)=-1/4*(-2)^2=-1/4*4=-1
=>A thuộc (P)
4: tính chất:
Nếu a>0 thì hàm số đồng biến khi x>0 và nghịch biến khi x<0
Nếu a<0 thì hàm số đồng biến khi x<0 và nghịch biến khi x>0
y=1/2x^2: Hàm số đồng biến khi x>0 và nghịch biến khi x<0
y=-3x^2: Hàm số đồng biến khi x<0 và nghịch biến khi x>0

a) Hệ đã cho vô nghiệm bởi vì mỗi nghiệm của hệ là nghiệm chung của hai phương trình, một phương trình vô nghiệm thì hệ không có nghiệm chung.
b) Hệ đã cho có vô số nghiệm.
Đáp án C
Tập nghiệm phương trình -2x + y = -3 được biểu diễn bởi đường thẳng -2x + y = -3
Tập nghiệm phương trình 3x – 2y = 7 được biểu diễn bởi đường thẳng 3x – 2y = 7
Ta có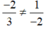 ⇒ phương trình có một nghiệm duy nhất
⇒ phương trình có một nghiệm duy nhất