Số vô tỉ:

Số vô tỉ là số không thể biểu diễn dưới dạng tập hợp các phân số  với  a, b là số nguyên và b # 0. Hay nói cách khác là số vô tỉ không thể biểu diễn dưới dạng tỉ số. Một số vô tỉ hoặc là số siêu việt hoặc là số đại số, trong đó hầu hết các số vô tỉ đều là số siêu việt và số siêu việt là số vô tỉ.

Tập hợp số vô tỉ ký hiệu là 

VD:

Số thực:

Số thực là tập hợp các số hữu tỉ và vô tỉ.

Tập hợp số thực kí hiệu là R

VD:Số nguyên là 35 còn số thực là số pi (3,141592…)

Chúc bạn học tốt ^^

Số trung bình cộng của dấu hiệu sẽ bằng số trung bình cộng ban đầu nhân với 8 luôn bởi vì nhân như vậy thì ta lấy số 8 ra làm nhân tử chung thì phần còn lại ở trên tử và dưới mẫu sẽ là trung bình cộng ban đầu

Để tính số trung bình cộng của các giá trị của dấu hiệu (nếu số đơn vị điều tra khá lớn) ta lập thêm trong bảng tần số một cột (dòng) ghi các tích mỗi giá trị nhân với tần số tương ứng của chúng.

- Tính tổng các số cột (dòng) tích

- Lấy tổng vừa tính được ở trên chia cho N.

Công thức tính số trung bình cộng:

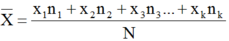Trong đó:

    x1, x2, ..., xk là k giá trị khác nhau của dấu hiệu x

    n1, n2, ..., nk là k tần số tương ứng

    N là số các giá trị

Ý nghĩa: Số trung bình cộng thường được dùng làm "đại diện" cho dấu hiệu, đặc biệt là khi muốn so sánh các dấu hiệu cùng loại.

Nếu trong dãy các giá trị của dấu hiệu có những giá trị có khoảng cách chênh lệch khá lớn thì lấy số trung bình cộng làm giá trị đại diện cho dấu hiệu không có ý nghĩa thực tế.

Giả sử các giá trị của dấu hiệu lần lượt là x₁ , x₂ , .... , x_k 

Tần số lần lượt tương ứng là n₁ , n₂ , .... , n_k 

Ta có số trung bình cộng ban đầu là: \(\overline{X}=\frac{x_1.n_1+x_2.n_2+....+x_k.n_k}{N}\)

Sau khi các giá trị của dấu hiệu giảm đi cùng một số a thì trung bình cộng mới là: 

\(\frac{\left(x_1-a\right).n_1+\left(x_2-a\right).n_2+....+\left(x_k-a\right).n_k}{N}=\frac{x_1.n_1-an_1+x_2.n_2-an_2+....+x_k.n_k-an_k}{N}\)

\(=\frac{\left(x_1.n_1+x_2.n_2+....+x_k.n_k\right)-a\left(n_1+n_2+...+n_k\right)}{N}\)

\(=\frac{\left(x_1.n_1+x_2.n_2+....+x_k.n_k\right)}{N}-\frac{a\left(n_1+n_2+...+n_k\right)}{N}\)

\(=\overline{X}-\frac{a.N}{N}=\overline{X}-a\)

Vậy khi các giá trị của dấu hiệu giảm đi cùng một số a thì số trung bình cộng của dấu hiệu cũng giảm đi a

Đuợc kí hiệu la (N) chữ hoa nhé

ki hieu chu N

Hình đâu ạ?

Cho mình hỏi hình ở đâu ak

Ko có hình ko làm đc đâu