
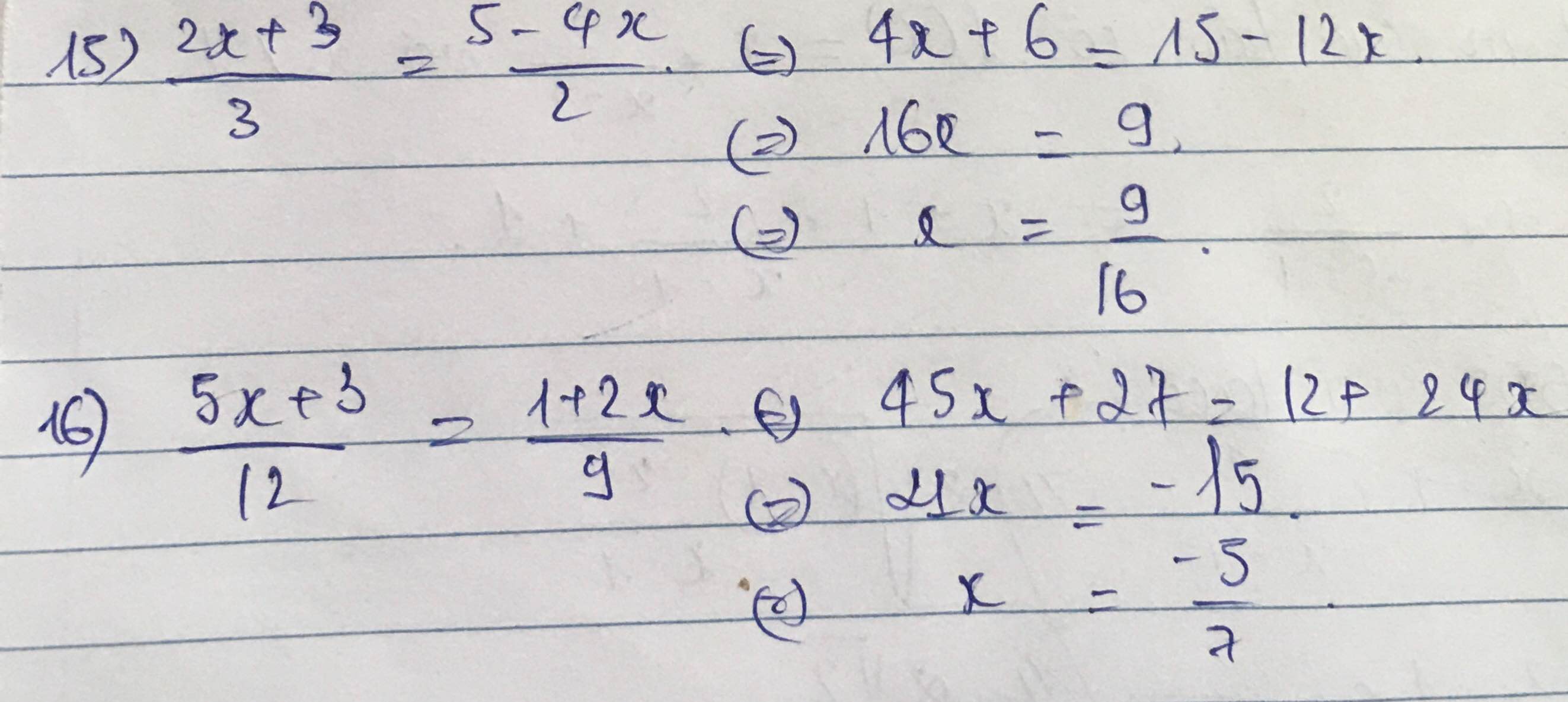
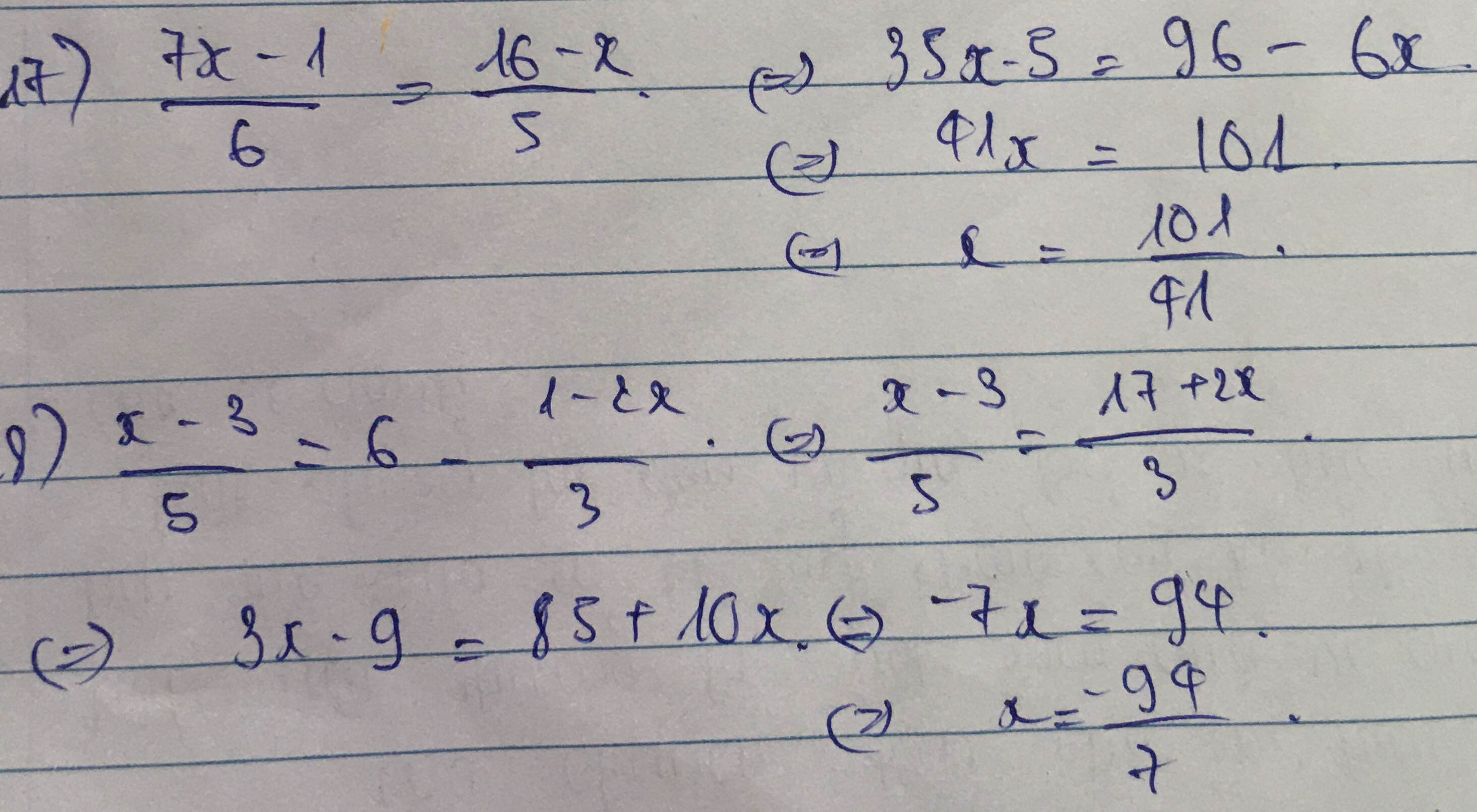
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

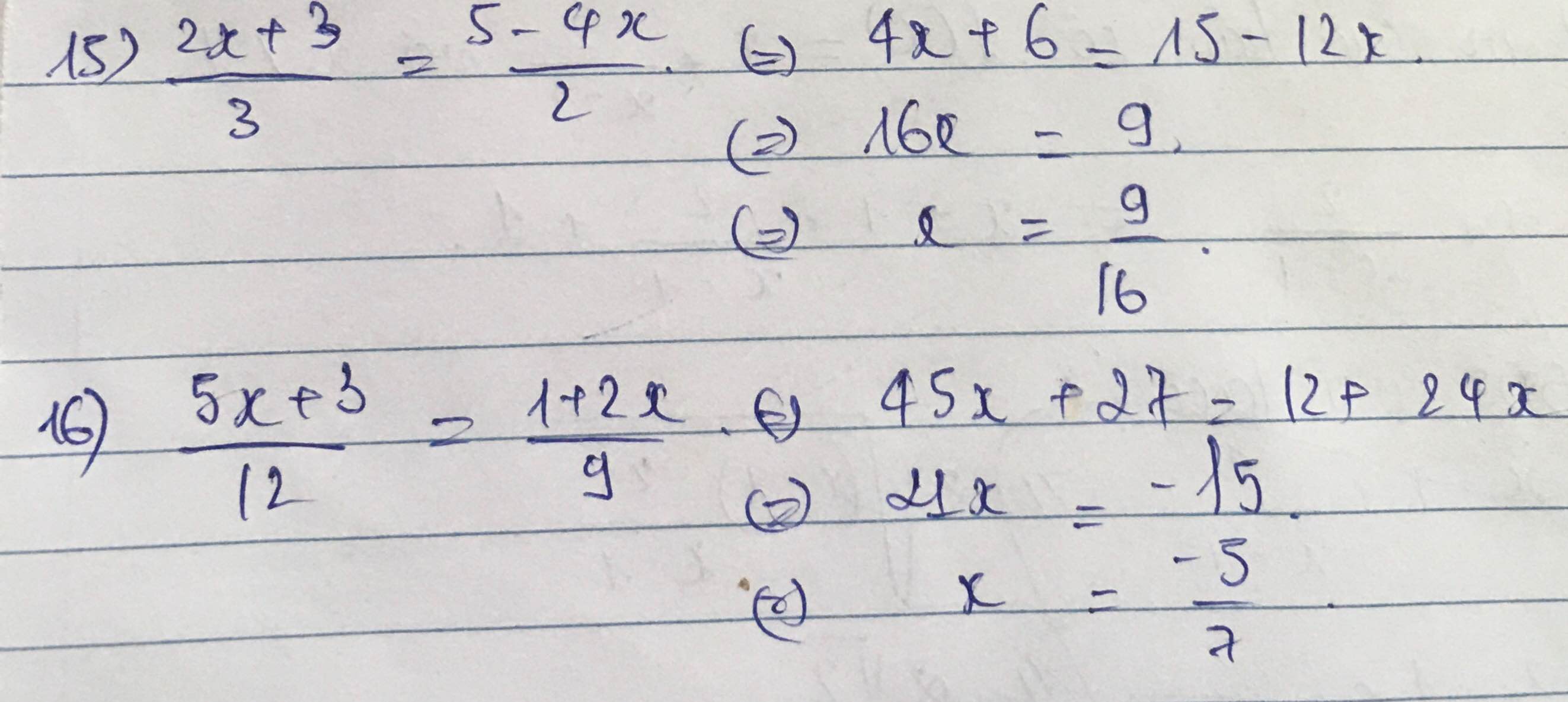
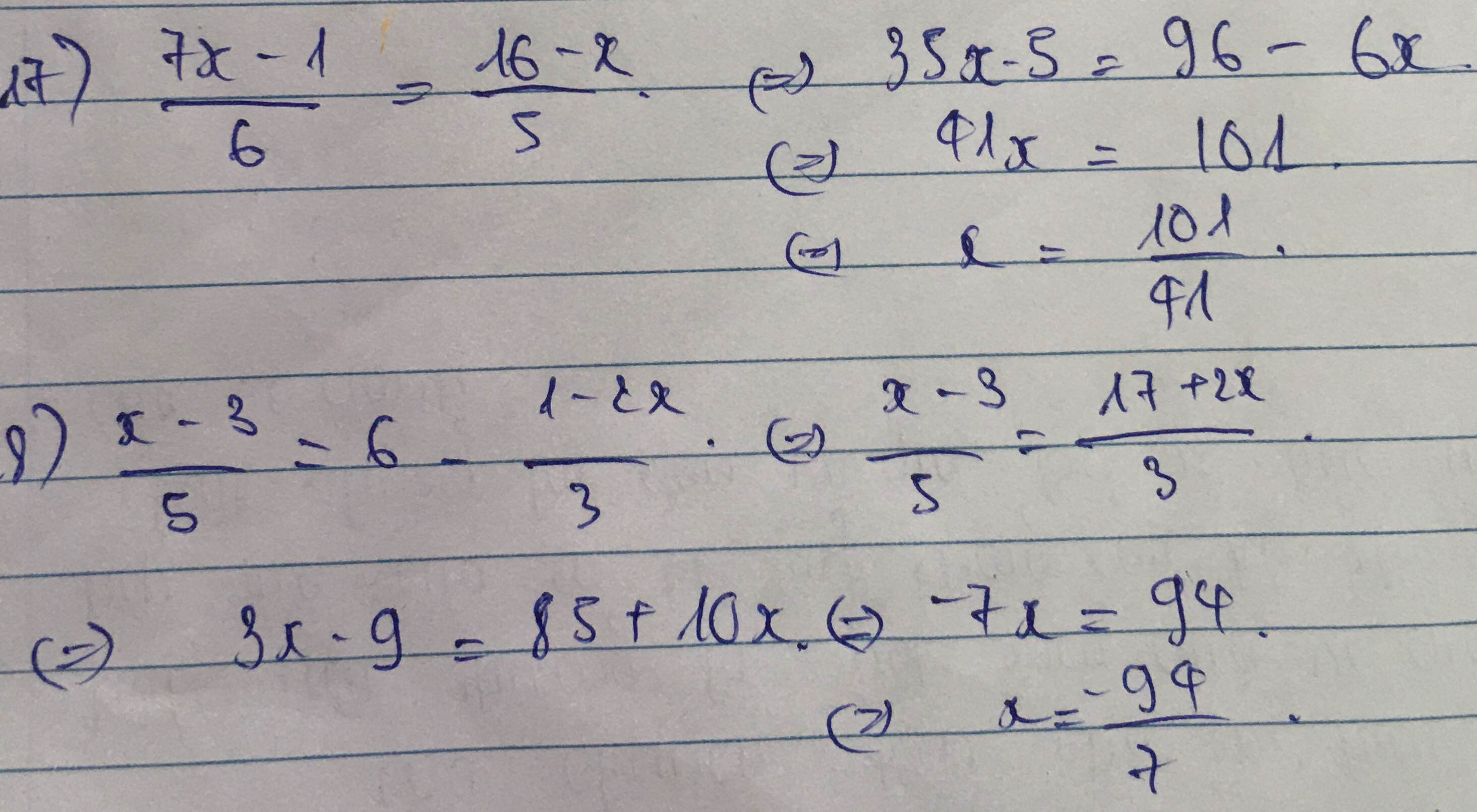

a )n = 0 => (1) = 9 .1 + 18 = 27 chia hết cho 27
n = 1 => (1) = 9 .10 + 18 = 108 chia hết cho 27
đặt k = n , ta giả sử 9.10^k + 18 chia hết cho 27
ta chứng minh 9.10^(k + 1) +18 chia hết cho 27
= 10.9.10^(k) +18 = 9.10^k + 18 + 9.9.10^k = { 9.10^k + 18 } + { 81.10^k }
cả 2 nhóm đều chia hết cho 27 => đpcm
b ) - Với \(n=1\) thì \(16^n-15n-1=16-15-1=0⋮225\)
- Gỉa sử \(16^k-15k-1⋮225\)
- Ta chứng minh \(16^{k+1}-15\left(k+1\right)-1⋮225\)
Thực vậy : \(16^{k+1}-15\left(k+1\right)-1=16.16^k-15k-15-1\)
\(=\left(16^k-15k-1\right)+15.16^k-15\)
Theo giả thuyết qui nạp \(16^k-15k-1⋮225\)
Còn \(15.16^k-15=15\left(16^k-1\right)⋮15.15=225\)
Vậy \(16^n-15n-1⋮225\)

18.
Áp dụng BĐT quen thuộc: \(\dfrac{1}{1+x^2}+\dfrac{1}{1+y^2}\ge\dfrac{2}{1+xy}\) ta có:
\(\dfrac{1}{1+a^3}+\dfrac{1}{1+b^3}\ge\dfrac{2}{1+\sqrt{a^3b^3}}\) ; \(\dfrac{1}{1+c^3}+\dfrac{1}{1+abc}\ge\dfrac{2}{1+\sqrt{abc^4}}\)
Cộng vế:
\(\dfrac{1}{1+a^3}+\dfrac{1}{1+b^3}+\dfrac{1}{1+c^3}+\dfrac{1}{1+abc}\ge2\left(\dfrac{1}{1+\sqrt{a^3b^3}}+\dfrac{1}{1+\sqrt{abc^4}}\right)\ge2\left(\dfrac{2}{1+\sqrt[4]{a^4b^4c^4}}\right)\)
\(\Rightarrow\dfrac{1}{1+a^3}+\dfrac{1}{1+b^3}+\dfrac{1}{1+c^3}+\dfrac{1}{1+abc}\ge\dfrac{4}{1+abc}\)
\(\Rightarrow\dfrac{1}{1+a^3}+\dfrac{1}{1+b^3}+\dfrac{1}{1+c^3}\ge\dfrac{3}{1+abc}\) (đpcm)
19.
Biến đổi tương đương:
\(\Leftrightarrow\left(a^2+b^2\right)xy+ab\left(x^2+y^2\right)\ge\left(a^2+b^2+2ab\right)xy\)
\(\Leftrightarrow\left(a^2+b^2\right)xy+ab\left(x^2+y^2\right)\ge\left(a^2+b^2\right)xy+2abxy\)
\(\Leftrightarrow ab\left(x^2+y^2\right)-2abxy\ge0\)
\(\Leftrightarrow ab\left(x^2+y^2-2xy\right)\ge0\)
\(\Leftrightarrow ab\left(x-y\right)^2\ge0\)

45^2+40^2-15^2+80.45
=45^2+80.45+40^2-15^2
=45^2+2.40.45+40^2-15^2
=(45+40)^2-15^2
=85^2-15^2
=(85+15)(85-15)
=100.70
=7000
cách 2
45^2+40^2-15^2+80.45
=45^2+80.45+40^2-15^2
=45^2+2.40.45+40^2-15^2
=(45+40)^2-15^2
=85^2-15^2
=(85+15)(85-15)
=100.70
=7000
ủng hộ nha!!!

a, Vì ME//AC hay ME//AF; MF//AB hay MF//AE nên AEMF là hbh
b, Vì M là trung điểm BC, MF//AB nên F là trung điểm AC
Do đó MF là đtb tg ABC \(\Rightarrow MF=\dfrac{1}{2}AB=4\left(cm\right)\)
c, Vì I đx M qua F nên \(MI=2MF=AB\left(MF=\dfrac{1}{2}AB\right)\)
Mà MF//AB (MF là đtb tg ABC) nên MI//AB
Do đó AIMB là hbh nên AI//BC
d, Gọi giao của AM và EF là G
Mà AEMF là hbh nên G là trung điểm AM,EF
Mà AIMB là hbh nên G là trung điểm IB
DO đó AM,EF,IB đồng quy tại G

Giải:
Gọi x là năng suất dự tính của xí nghiệp (sản phẩm/ngày); (x ∈ N*) .
⇒ Số thảm len dệt được theo dự tính là: 20x (thảm).
Sau khi cải tiến, năng suất của xí nghiệp đã tăng 20% nên năng suất trên thực tế là:
x + 20%.x = x + 0,2x = 1,2x (sản phẩm/ngày)
Sau 18 ngày, xí nghiệp dệt được:
18.1,2x = 21,6.x (thảm).
Vì sau 18 ngày, xí nghiệp không những hoàn thành số thảm cần dệt mà còn dệt thêm được 24 tấm nên ta có phương trình:
21,6.x = 20x + 24
⇔ 21,6x – 20x = 24
⇔ 1,6x = 24
⇔ x = 15 (thỏa mãn)
Vậy số thảm mà xí nghiệp phải dệt ban đầu là: 20.15 = 300 (thảm).

9.
\(\Leftrightarrow a^2+a^2b^2+b^2+b^2c^2+c^2+c^2a^2\ge6abc\)
\(\Leftrightarrow\left(a^2-2abc+b^2c^2\right)+\left(b^2-2abc+c^2a^2\right)+\left(c^2-2abc+a^2b^2\right)\ge0\)
\(\Leftrightarrow\left(a-bc\right)^2+\left(b-ca\right)^2+\left(c-ab\right)^2\ge0\) (luôn đúng)
Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(0;0;0\right);\left(1;1;1\right);\left(1;-1;-1\right)\) và các hoán vị
10.
\(a^2+b^2+c^2=1\)
\(\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=1+2\left(ab+bc+ca\right)\)
\(\Leftrightarrow\left(a+b+c\right)^2=1+2\left(ab+bc+ca\right)\)
\(\Rightarrow1+2\left(ab+bc+ca\right)\ge0\Rightarrow ab+bc+ca\ge-\dfrac{1}{2}\)
Lại có:
\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)
\(\Leftrightarrow a^2+b^2+c^2\ge ab+bc+ca\)
\(\Rightarrow ab+bc+ca\le1\)
11.
Do \(a^2+b^2+c^2=1\Rightarrow\left\{{}\begin{matrix}\left|a\right|\le1\\\left|b\right|\le1\\\left|c\right|\le1\end{matrix}\right.\) \(\Rightarrow\left(a+1\right)\left(b+1\right)\left(c+1\right)\ge0\)
Do đó:
\(abc+2\left(1+a+b+c+ab+bc+ca\right)\)
\(=1+a+b+c+ab+bc+ca+\left(1+a+b+c+ab+bc+ca+abc\right)\)
\(=\dfrac{1}{2}\left(a^2+b^2+c^2\right)+ab+bc+ca+a+b+c+\dfrac{1}{2}+\left(a+1\right)\left(b+1\right)\left(c+1\right)\)
\(=\dfrac{1}{2}\left(a+b+c\right)^2+\left(a+b+c\right)+\dfrac{1}{2}+\left(a+1\right)\left(b+1\right)\left(c+1\right)\)
\(=\dfrac{1}{2}\left(a+b+c+1\right)^2+\left(a+1\right)\left(b+1\right)\left(c+1\right)\ge0\) (đpcm)

\(5\left(18-5x\right)-12\left(3x-7\right)=15\left(2x-16\right)-6\left(x+14\right)\)
\(90-25x-36x+84=30x-240-6x-84\)
\(90+84+240+84=30x-6x+36x+25x\)
\(498=85x\)
\(x=\frac{498}{85}\)