
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1.
\(\left\{{}\begin{matrix}x_{A'}=x_A+\left(-1\right)=2\\y_{A'}=y_A+3=0\end{matrix}\right.\) \(\Rightarrow A'\left(2;0\right)\)
2.
\(\overrightarrow{MP}=\left(4;2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_{N'}=x_N+4=-4+4=0\\y_{N'}=y_N+2=1+2=3\end{matrix}\right.\)
\(\Rightarrow N'\left(0;3\right)\)
3.
\(\overrightarrow{MM'}=\left(13;7\right)\Rightarrow\overrightarrow{v}=\overrightarrow{MM'}=\left(13;7\right)\)
4.
\(\overrightarrow{MN}=\left(-2;-1\right)\Rightarrow MN=\sqrt{\left(-2\right)^2+\left(-1\right)^2}=\sqrt{5}\)
\(\Rightarrow M'N'=MN=\sqrt{5}\)
5.
Gọi G là trọng tâm ABC \(\Rightarrow G\left(2;1\right)\)
\(\overrightarrow{BC}=\left(-6;-3\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_{G'}=2-6=-4\\y_{G'}=1-3=-2\end{matrix}\right.\) \(\Rightarrow G'\left(-4;-2\right)\)

Do d' là ảnh của d qua phép tịnh tiến nên d' cùng phương với d
\(\Rightarrow\) Phương trình d' có dạng: \(x-2y+c=0\)
Chọn \(A\left(-1;0\right)\) là 1 điểm thuộc d
Gọi \(A'\left(x';y'\right)\) là ảnh của A qua phép tịnh tiến \(\overrightarrow{v}\Rightarrow A'\in d'\)
\(\left\{{}\begin{matrix}x'=-1+\left(-1\right)=-2\\y'=0+3=3\end{matrix}\right.\) \(\Rightarrow A'\left(-2;3\right)\)
Thế vào pt d':
\(-2-2.3+c=0\Rightarrow c=8\)
Vậy pt d' có dạng: \(x-2y+8=0\)

Câu 1: Ý C
PT \(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\) mà\(x\in\left(0;2\pi\right)\)
Có 3 nghiệm
Câu 2: Ý A
PT \(\Leftrightarrow\left[{}\begin{matrix}sinx=1\\sinx=\dfrac{1}{2}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\) mà \(0\le x< \dfrac{\pi}{2}\)
\(\Rightarrow x=\dfrac{\pi}{6}\)


1.
\(y'=\left(cos^2\left(2x+3\right)\right)'=2cos\left(2x+3\right).\left(cos\left(2x+3\right)\right)'\)
\(=2cos\left(2x+3\right).\left(-sin\left(2x+3\right)\right).\left(2x+3\right)'\)
\(=-4sin\left(2x+3\right).cos\left(2x+3\right)\)
\(=-4sin\left(4x+6\right)\)
2.
\(f'\left(x\right)=-x^2+\left(3m-2\right)x-\left(2m^2-5m-2\right)\)
Để \(f'\left(x\right)< 0;\forall x\in R\)
\(\Leftrightarrow\Delta=\left(3m-2\right)^2-4\left(2m^2-5m-2\right)< 0\)
\(\Leftrightarrow m^2+8m+12< 0\)
\(\Rightarrow-6< m< -2\)

5.
\(y=\dfrac{2x-1}{1-x}\Rightarrow y'=\dfrac{\left(2x-1\right)'\left(1-x\right)-\left(1-x\right)'\left(2x-1\right)}{\left(1-x\right)^2}\)
\(=\dfrac{2\left(1-x\right)+\left(2x-1\right)}{\left(1-x\right)^2}=\dfrac{1}{\left(1-x\right)^2}=\dfrac{1}{\left(x-1\right)^2}\)
9.
\(\lim\limits\dfrac{2n^2+4}{3-n^2}=\lim\dfrac{2+\dfrac{4}{n^2}}{\dfrac{3}{n^2}-1}=\dfrac{2+0}{0-1}=-2\)

2.
Xét khai triển:
\(\left(1+x\right)^{2017}=C_{2017}^0+C_{2017}^1.x+C_{2017}^2x^2+...+C_{2017}^{2017}x^{2017}\)
Cho \(x=1\) ta được:
\(2^{2017}=C_{2017}^0+C_{2017}^1+...+C_{2017}^{2017}\)
\(\Rightarrow C_{2017}^1+C_{2017}^2+...+C_{2017}^{2017}=2^{2017}-C_{2017}^0=2^{2017}-1\)
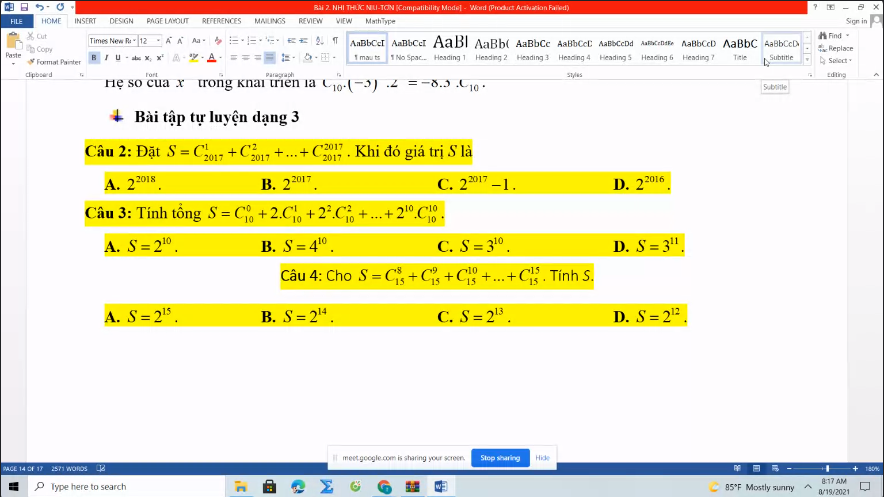
3.
Xét khai triển:
\(\left(1+x\right)^{10}=C_{10}^0+C_{10}^1x+...+C_{10}^{10}x^{10}\)
Thay \(x=2\) ta được:
\(3^{10}=C_{10}^0+2C_{10}^1+2^2C_{10}^2+...+2^{10}C_{10}^{10}\)
\(\Rightarrow S=3^{10}\)
4.
Xét khai triển:
\(\left(1+x\right)^{15}=C_{15}^0+C_{15}^1x+...+C_{15}^{15}x^{15}\)
Thay \(x=1\) ta được:
\(2^{15}=C_{15}^0+C_{15}^1+...+C_{15}^{15}\)
Mặt khác, áp dụng công thức: \(C_n^k=C_n^{n-k}\) ta có:
\(C_{15}^0=C_{15}^{15}\)
\(C_{15}^1=C_{15}^{14}\)
...
\(C_{15}^7=C_{15}^8\)
Cộng vế:
\(C_{15}^0+C_{15}^1+...+C_{15}^7=C_{15}^8+C_{15}^9+...+C_{15}^{15}\)
\(\Rightarrow C_{15}^0+C_{15}^1+...+C_{15}^{15}=2\left(C_{15}^8+C_{15}^9+...+C_{15}^{15}\right)\)
\(\Rightarrow2S=2^{15}\)
\(\Rightarrow S=2^{14}\)



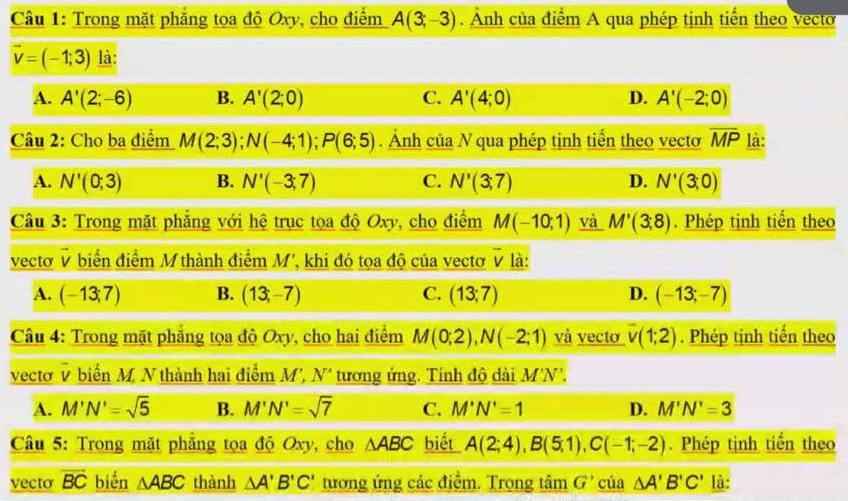


 mọi người giải giúp em theo phương pháp tự luận với ạ
mọi người giải giúp em theo phương pháp tự luận với ạ 


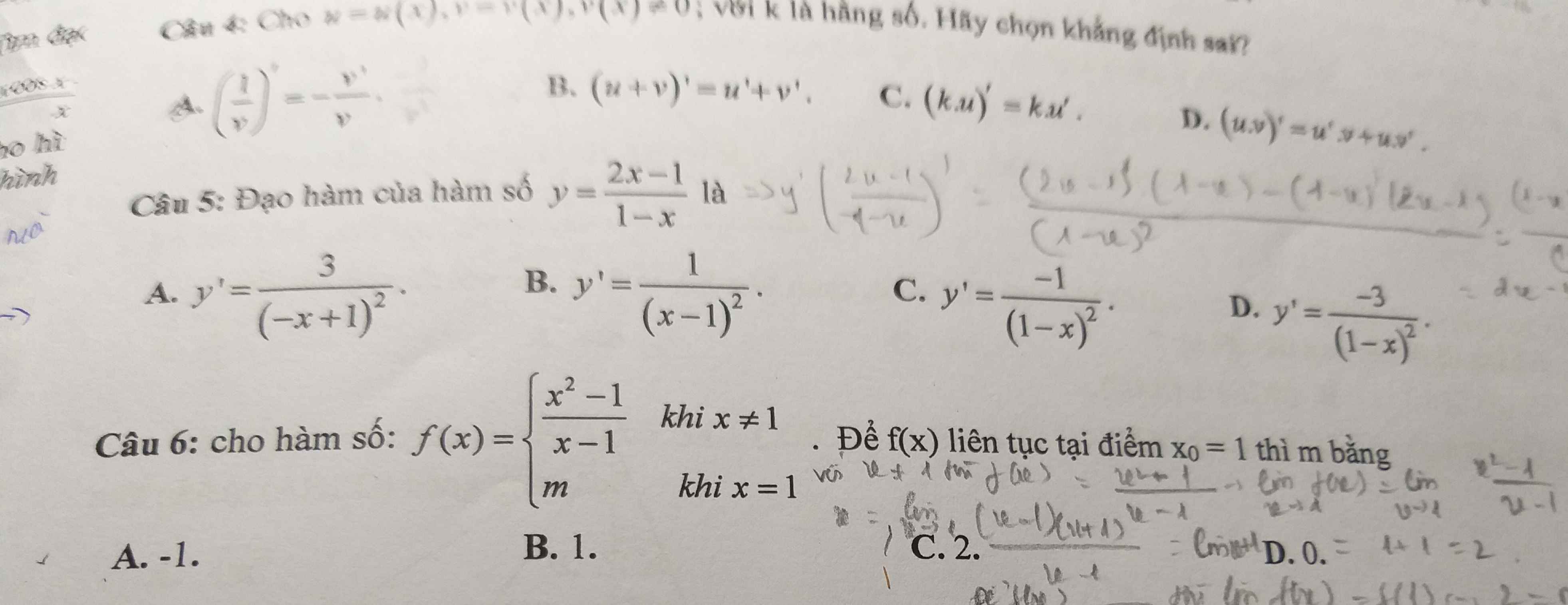


mỗi lần đăng chỉ được 1 câu hỏi tự luận thôi
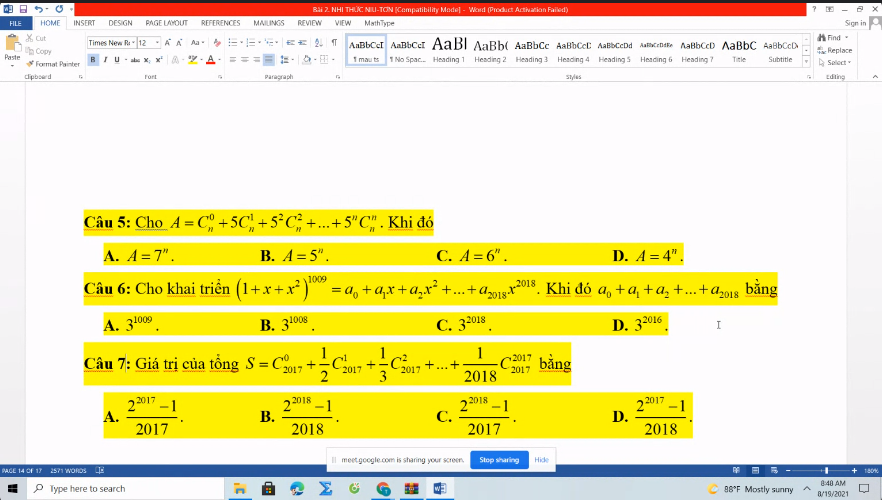
vậy giúp em bài 6 ạ