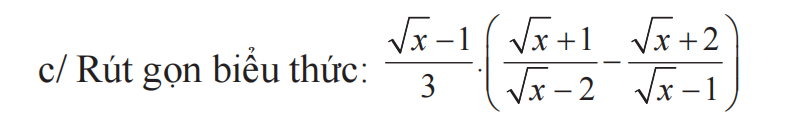Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
b. Tam giác $ABC$ vuông tại $A$ và $C=45^0$ nên:
$B=90^0-C=90^0-45^0=45^0$
Do đó, tam giác $ABC$ vuông cân tại $A$
$\Rightarrow AC=AB=50$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{50^2+50^2}=50\sqrt{2}$ (cm)
f.
Theo định lý Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{7^2-5^2}=2\sqrt{6}$ (cm)
$\sin B=\frac{AC}{BC}=\frac{2\sqrt{6}}{7}$
$\Rightarrow B=44,42^0$
$C=90^0-B=90^0-44,42^0=45,58^0$
b) Xét ΔABC vuông tại A có \(\widehat{C}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định nghĩa tam giác vuông cân)
Suy ra: \(\widehat{B}=45^0\) và AC=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=50^2+50^2=5000\)
hay \(BC=50\sqrt{2}\left(cm\right)\)

5.
\(\Delta=m^2-4\left(m-1\right)=\left(m-2\right)^2\)
Pt có 2 nghiệm pb khi \(\left(m-2\right)^2>0\Rightarrow m\ne2\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-1\end{matrix}\right.\)
\(x_1^2+x_2^2=x_1+x_2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=x_1+x_2\)
\(\Leftrightarrow m^2-2\left(m-1\right)=m\)
\(\Leftrightarrow m^2-3m+2=0\Rightarrow\left[{}\begin{matrix}m=1\\m=2\left(loại\right)\end{matrix}\right.\)
1.
\(\Delta=9+4m>0\Rightarrow m>-\dfrac{9}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-3\\x_1x_2=-m\end{matrix}\right.\)
\(5x_1+5x_2=1-\left(x_1x_2\right)^2\)
\(\Leftrightarrow5\left(x_1+x_2\right)=1-\left(x_1x_2\right)^2\)
\(\Leftrightarrow5.\left(-3\right)=1-\left(-m\right)^2\)
\(\Leftrightarrow m^2=16\Rightarrow\left[{}\begin{matrix}m=4\\m=-4< -\dfrac{9}{4}\left(loại\right)\end{matrix}\right.\)
2.
\(\Delta=\left(2m+1\right)^2-4\left(m^2+1\right)=4m-3>0\Rightarrow m>\dfrac{3}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m+1\\x_1x_2=m^2+1\end{matrix}\right.\)
\(\left(x_1+1\right)^2+\left(x_2+1\right)^2=13\)
\(\Leftrightarrow x_1^2+2x_1+1+x_2^2+2x_2+1=13\)
\(\Leftrightarrow x_1^2+x_2^2+2\left(x_1+x_2\right)=11\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\left(x_1+x_2\right)=11\)
\(\Leftrightarrow\left(2m+1\right)^2-2\left(m^2+1\right)+2\left(2m+1\right)=11\)
\(\Leftrightarrow2m^2+8m-10=0\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m=-5< \dfrac{3}{4}\left(loại\right)\end{matrix}\right.\)

Bài 3:
a:Ta có: \(\sqrt{4x^2-4x+1}=3\)
\(\Leftrightarrow\left|2x-1\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=3\\2x-1=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
b: Ta có: \(2\sqrt{x-1}-4=0\)
\(\Leftrightarrow x-1=4\)
hay x=5


Lời giải:
Đổi $3h15'$ thành $3,25$ giờ
Trong 1 giờ:
Vòi thứ nhất chảy được: $\frac{1}{4,5}$ (bể)
Vòi thứ hai chảy được: $\frac{1}{3,25}$ (bể)
Trong 1 giờ thì cả hai vòi cùng chảy được: $\frac{1}{4,5}+\frac{1}{3,25}=\frac{62}{117}$ (bể)
Hai vòi cùng chảy thì sẽ đầy bể sau:
$1:\frac{62}{117}=\frac{117}{62}$ giờ
Đổi $\frac{117}{62}$ giờ thành $1$ giờ $53$ phút $14$ giây


b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x+1=x-2\\y=x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-5\end{matrix}\right.\)

c) \(\dfrac{\sqrt{x}-1}{3}\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\right)\)
\(=\dfrac{\sqrt{x}-1}{3}.\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{\sqrt{x}-1}{3}.\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\)
\(=\dfrac{x-1}{3\left(\sqrt{x}-2\right)}-\dfrac{\sqrt{x}+2}{3}\)
\(=\dfrac{x-1}{3\left(\sqrt{x}-2\right)}-\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{3\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-1}{3\left(\sqrt{x}-2\right)}-\dfrac{x-4}{3\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-1-x+4}{3\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3}{3\left(\sqrt{x}-2\right)}\)
\(=\dfrac{1}{\sqrt{x}-2}\)
bt trong dấu ngoặc bn nhân lên hợp ⇒ rút gọn ⇒ nhân với bt ngoài dấu ngoặc ⇒ rút gọn thôi á
mk gợi ý vậy thôi nha, chứ h giải ra thì lâu lắm=((
chúc bn làm bài tốt nka^3^
 Làm giúp mình trước 1.15 nha cảm ơn ạ :((
Làm giúp mình trước 1.15 nha cảm ơn ạ :((

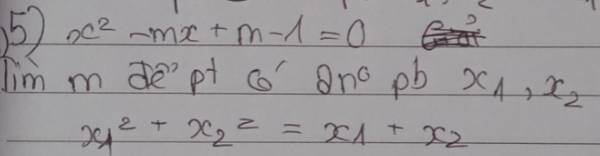
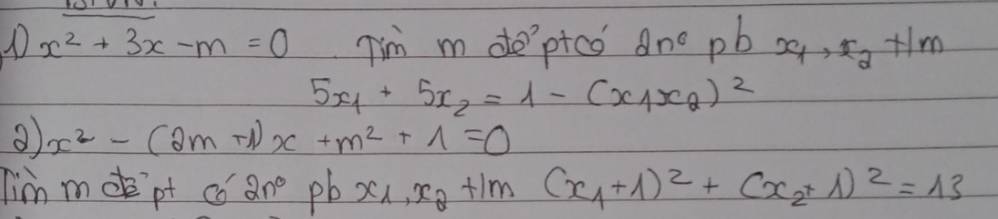
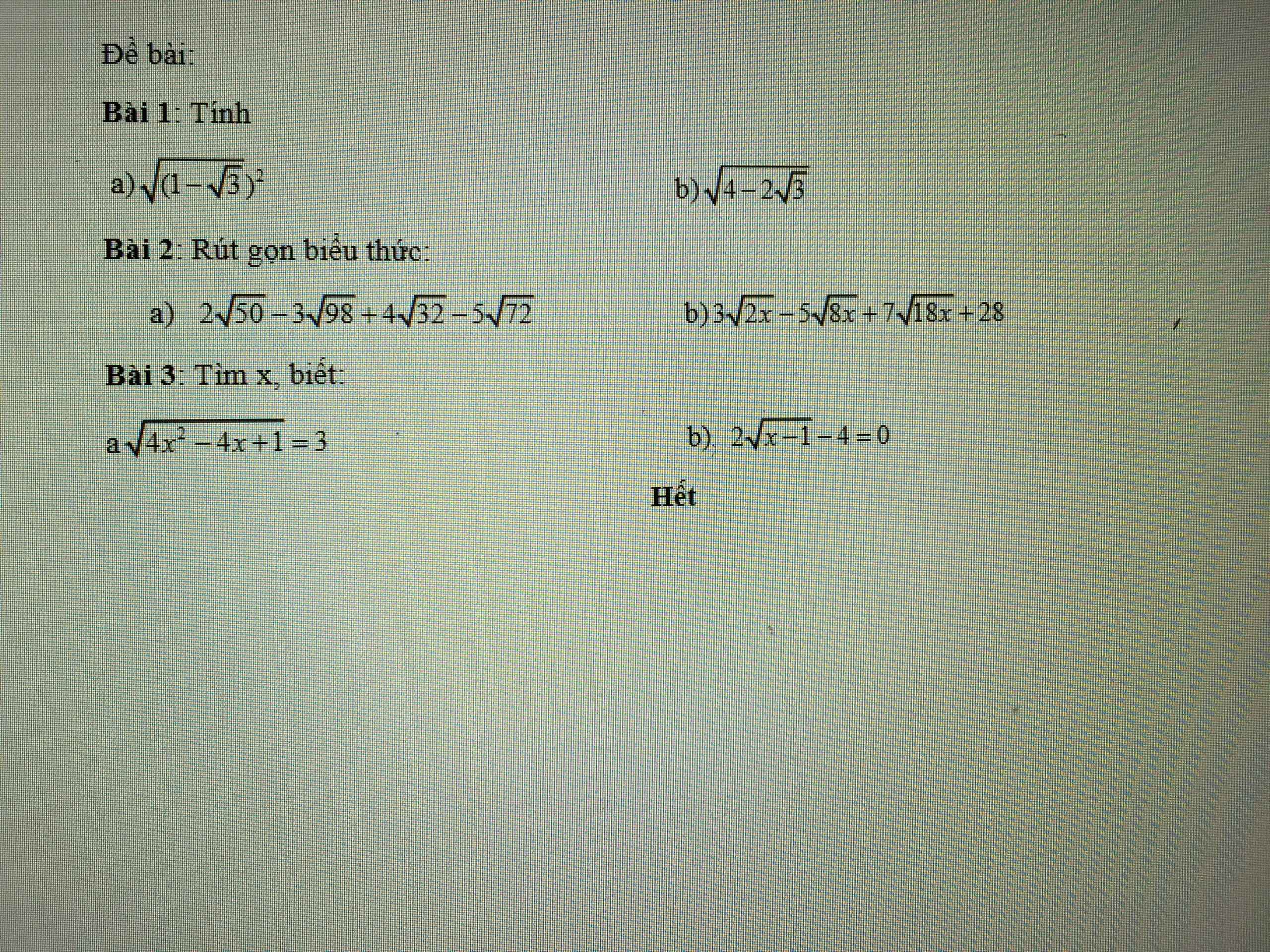 Giúp mình vs ạ. Cảm ơn trước ạ!
Giúp mình vs ạ. Cảm ơn trước ạ!