
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{x-2\sqrt{x}}{x-4}=\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}}{\sqrt{x}+2}\)

\(P=\left(\frac{1}{\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+1}\right):\frac{\sqrt{x}}{x+\sqrt{x}}\)ĐK : x > 0
\(=\left(\frac{\sqrt{x}+1+x}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\frac{1}{\sqrt{x}+1}=\frac{x+\sqrt{x}+1}{\sqrt{x}}\)
\(P=\frac{\sqrt{x}}{\sqrt{x}-1}+\frac{3}{\sqrt{x}+1}-\frac{6\sqrt{x}-4}{x-1}\)
\(=\frac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}+4}{x-1}=\frac{x-2\sqrt{x}+1}{x-1}=\frac{\sqrt{x}-1}{\sqrt{x}+1}\)

b: B>0
=>\(\dfrac{1}{-x+\sqrt{x}}>0\)
=>\(-x+\sqrt{x}>0\)
=>\(x-\sqrt{x}< 0\)
=>\(\sqrt{x}\left(\sqrt{x}-1\right)< 0\)
=>\(\sqrt{x}-1< 0\)
=>\(\sqrt{x}< 1\)
=>0<=x<1
Kết hợp ĐKXĐ, ta được: 0<x<1

\(A=\left(\sqrt{2}-8\sqrt{32}+2\sqrt{450}\right):\left(-3\sqrt{8}\right)\)
\(=\left(\sqrt{2}-32\sqrt{2}+30\sqrt{2}\right):\left(-6\sqrt{2}\right)\)
\(=\sqrt{2}\left[\left(1-32+30\right):\left(-6\right)\right]\)
\(=\sqrt{2}\left[\left(-1\right):\left(-6\right)\right]\)
\(=\sqrt{2}.\dfrac{1}{6}\)
\(=\dfrac{\sqrt{2}}{6}\)

\(a,=\dfrac{-\sqrt{a}\left(1-\sqrt{a}\right)}{1-\sqrt{a}}=-\sqrt{a}\\ b,=\dfrac{\sqrt{p}\left(\sqrt{p}-2\right)}{\sqrt{p}-2}=\sqrt{p}\)

ĐKXĐ: \(x\ge0;x\ne4\)
\(A=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}-\dfrac{3\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}-\dfrac{12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+4\sqrt{x}+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}-\dfrac{3\sqrt{x}-6}{\left(\sqrt{x}+2\right)\left(\sqrt{x}+2\right)}-\dfrac{12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+4\sqrt{x}+4-3\sqrt{x}+6-12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}-2}\)

\(C=\left(\dfrac{3}{x-1}+\dfrac{1}{\sqrt{x}+1}\right):\dfrac{1}{\sqrt{x}+1}\)
\(=\dfrac{3+\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+1}{1}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\)

2b)
xét vế trái ta có
=\(\left(\sqrt{x}-\sqrt{y}\right).\dfrac{\sqrt{x^2y}+\sqrt{xy^2}}{\sqrt{xy}}\) \(\left(\sqrt{x}-\sqrt{y}\right).\dfrac{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{xy}}\)=x-y
3b)
để A<0 \(\Rightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}}< 0\)
\(\Rightarrow\sqrt{x}-1< 0\)\(\Rightarrow\sqrt{x}< 1\)\(\Rightarrow x< 1\)
a: Ta có: \(\sqrt{9x^2-6x+1}=5\)
\(\Leftrightarrow\left|3x-1\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=5\\3x-1=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=6\\3x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{4}{3}\end{matrix}\right.\)
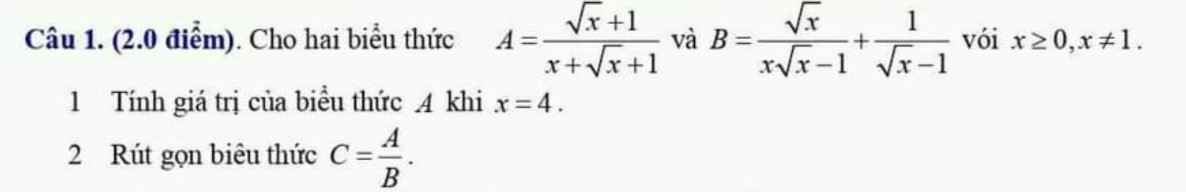

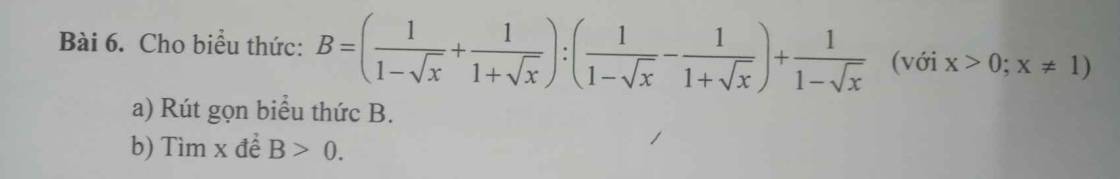 Câu (a) đã rút gọn được là
Câu (a) đã rút gọn được là 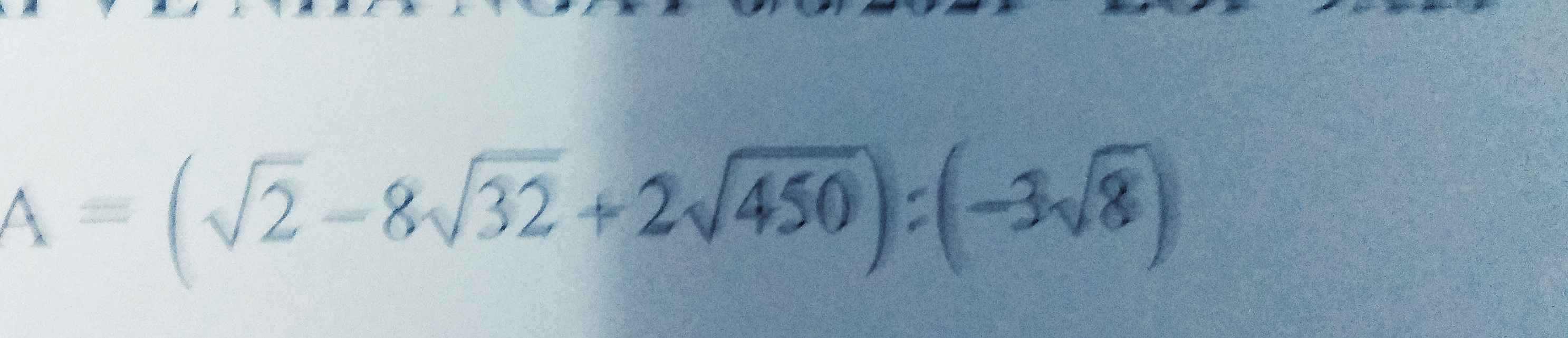
 giúp mik với ạ chỉ cần rút gọn 6 cái biểu thức thui ạ .mong mn giúp đỡ.
giúp mik với ạ chỉ cần rút gọn 6 cái biểu thức thui ạ .mong mn giúp đỡ.
Với `x >= 0,x \ne 1` có:
`C=A/B=A:B=[\sqrt{x}+1]/[x+\sqrt{x}+1]:(\sqrt{x}/[x\sqrt{x}-1]+1/[\sqrt{x}-1])`
`C=[\sqrt{x}+1]/[x+\sqrt{x}+1]:[\sqrt{x}+x+\sqrt{x}+1]/[(\sqrt{x}-1)(x+\sqrt{x}+1)]`
`C=[\sqrt{x}+1]/[x+\sqrt{x}+1].[(\sqrt{x}-1)(x+\sqrt{x}+1)]/[x+2\sqrt{x}+1]`
`C=[\sqrt{x}+1]/[x+\sqrt{x}+1].[(\sqrt{x}-1)(x+\sqrt{x}+1)]/[(\sqrt{x}+1)^2]`
`C=[\sqrt{x}-1]/[\sqrt{x}+1]`
1.Thế \(x=4\) vào A, ta được:
\(A=\dfrac{\sqrt{4}+1}{4+\sqrt{4}+1}=\dfrac{2+1}{4+2+1}=\dfrac{3}{7}\)
2.
\(B=\dfrac{\sqrt{x}}{x\sqrt{x}-1}+\dfrac{1}{\sqrt{x}-1}\)
\(B=\dfrac{\sqrt{x}}{\sqrt{x}^3-1}+\dfrac{1}{\sqrt{x}-1}\)
\(B=\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{1}{\sqrt{x}-1}\)
\(B=\dfrac{\sqrt{x}+\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(B=\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(B=\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(C=\dfrac{A}{B}\)
\(C=\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}:\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(C=\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}.\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2}\)
\(C=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)