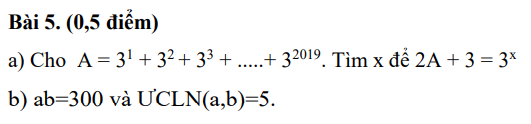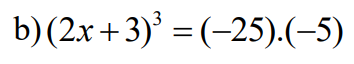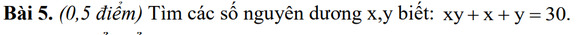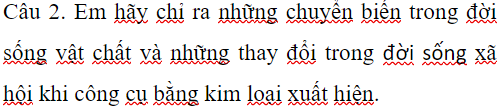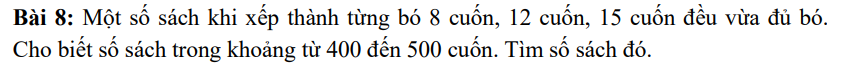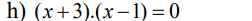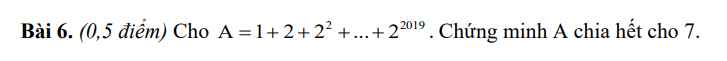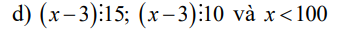\(\left(2x+3\right)^3=\left(-25\right).\left(-5\right)\)

\(\Leftrightarrow\left(2x+3\right)^3=125\)

\(\Leftrightarrow\left(2x+3\right)^3=5^3\)

\(\Leftrightarrow2x+3=5\)

\(\Leftrightarrow2x=2\)

\(\Leftrightarrow x=1\)

\(\left(2x+3\right)^3=\left(-25\right).\left(-5\right)\)

\(\Leftrightarrow\left(2x+3\right)^3=5^3\)

\(\Leftrightarrow2x+3=5\)

\(\Leftrightarrow2x=2\)

\(\Leftrightarrow x=1\)

\(\Leftrightarrow x\left(y+1\right)+y+1=31\\ \Leftrightarrow\left(x+1\right)\left(y+1\right)=31=31\cdot1\)

\(TH_1:\left\{{}\begin{matrix}x+1=31\\y+1=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=30\\y=0\end{matrix}\right.\rightarrow\left(30;0\right)\\ TH_2:\left\{{}\begin{matrix}x+1=1\\y+1=31\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=30\end{matrix}\right.\rightarrow\left(0;30\right)\)

Vậy \(\left(x;y\right)\in\left\{\left(30;0\right);\left(0;30\right)\right\}\)

\(\Leftrightarrow xy+x+y+1=31\Leftrightarrow\left(x+1\right)\left(y+1\right)=31\)

Do x, y nguyên dương nên xảy ra các TH sau:

TH1: \(\left\{{}\begin{matrix}x+1=1\\y+1=31\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=30\end{matrix}\right.\)(LOẠI)

TH2:\(\left\{{}\begin{matrix}x+1=31\\y+1=1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=30\\y=0\end{matrix}\right.\)(LOẠI)

Vậy không có x, y nguyên dương thoả mãn đề bài.

b: T=(-1)+(-1)+...+(-1)

=-1011

làm giúp mình câu a nữa nhé 'v'

Những chuyển biến trg đời sống vật chất:

+ Công cụ lđộng = kim loại dần thay thế công cụ đá

+ Nhiều ngành sản xuất mới xuất hiện: nông nghiệp dùng cày, chăn nuôi, nghề luyện kim, ...

=> Xuất hiện 1 lượng sản phẩm dư thừa

Sự thay đổi trg đời sống xã hội:

+ GĐ phụ hệ thay thế GĐ mẫu hệ

+ Xã hội phân hoá giàu - nghèo

=> Xã hội nguyên thuỷ tan rã hình thành xã hội có giai cấp

Gọi số sách là x

Theo đề, ta có: \(x\in BC\left(8;12;15\right)\)

hay x=480

x = -3 và x = 1 

\(\Leftrightarrow\left\{{}\begin{matrix}x+3=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\)

\(A=\left(1+2+2^2\right)+\left(2^3+2^4+2^5\right)+...+\left(2^{2017}+2^{2018}+2^{2019}\right)\\ A=\left(1+2+2^2\right)+2^3\left(1+2+2^2\right)+...+2^{2017}\left(1+2+2^2\right)\\ A=\left(1+2+2^2\right)\left(1+2^3+...+2^{2017}\right)\\ A=7\left(1+2^3+...+2^{2017}\right)⋮7\)

\(1+2+2^2+...+2^{2019}\\ =\left(1+2+2^2\right)+\left(2^3+2^4+2^5\right)+...+\left(2^{2017}+2^{2018}+2^{2019}\right)\\ =\left(1+2+2^2\right)+2^3\left(1+2+2^2\right)+...+2^{2017}\left(1+2+2^2\right)\\ =\left(1+2+2^2\right)\left(1+2^3+...+2^{2017}\right)\\ =7\left(1+2^3+...+2^{2017}\right)⋮7\)

\(\Rightarrow\left(x-3\right)\in BC\left(10,15\right)=B\left(30\right)=\left\{0;30;60;90;120;...\right\}\\ \Rightarrow x\in\left\{3;33;63;93;123;....\right\}\\ \text{Mà }x< 100\\ \Rightarrow x\in\left\{3;33;63;93\right\}\)