Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c) \(x-\dfrac{10}{3}=\dfrac{7}{15}\cdot\dfrac{3}{5}\)
\(x-\dfrac{10}{3}=\dfrac{7}{25}\)
\(x=\dfrac{7}{25}+\dfrac{10}{3}\)
\(x=\dfrac{271}{75}\)
d) \(x+\dfrac{3}{22}=\dfrac{27}{121}\div\dfrac{9}{11}\)
\(x+\dfrac{3}{22}=\dfrac{3}{11}\)
\(x=\dfrac{3}{11}-\dfrac{3}{22}\)
\(x\) \(=\dfrac{3}{22}\)
e) \(\dfrac{8}{23}\div\dfrac{24}{46}-x=\dfrac{1}{3}\)
\(\dfrac{2}{3}-x=\dfrac{1}{3}\)
\(x=\dfrac{2}{3}-\dfrac{1}{3}\)
\(x=\dfrac{1}{3}\)
f) \(1-x=\dfrac{49}{65}\cdot\dfrac{5}{7}\)
\(1-x=\dfrac{7}{13}\)
\(x=1-\dfrac{7}{13}\)
\(x=\dfrac{6}{13}\)

Số số hạng là :
( 50 - 5 ) : 5 + 1 = 10 ( số )
Tổng trên là :
( 50 + 5 ) . 10 : 2 = 275
Vậy,.............

Bài 1.2
1: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
2) Ta có: \(A=\dfrac{2\sqrt{x}}{\sqrt{x}+3}-\dfrac{\sqrt{x}+1}{3-\sqrt{x}}-\dfrac{3-11\sqrt{x}}{x-9}\)
\(=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{3-11\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{2x-6\sqrt{x}+x+4\sqrt{x}+3-3+11\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{3x+9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}-3}\)

a: Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: ED là đường trung bình của ΔABC
Suy ra: ED//BC và \(ED=\dfrac{BC}{2}\left(1\right)\)
Xét ΔGBC có
M là trung điểm của GB
N là trung điểm của GC
Do đó: MN là đường trung bình của ΔGBC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\left(2\right)\)
Từ (1), (2) suy ra ED//MN và ED=MN
Xét tứ giác EMND có
ED//MN
ED=MN
Do đó: EMND là hình bình hành
b: Ta có: \(ED=\dfrac{BC}{2}\)
mà \(MN=\dfrac{BC}{2}\)
nên ED=MN

`c)-x^2+7x-2=-(x^2-7x)-2`
`=-(x^2-7x+49/4-49/4)-2`
`=-(x-7/2)^2+49/4-2`
`=-(x-7/2)^2+41/4<=41/4`
Dấu "=" xảy ra khi `x=7/2`
`d)-4x^2+8x-9=-(4x^2-8x)-9`
`=-(4x^2-8x+4-4)-9`
`=-(2x-2)^2-5<=-5`
Dấu "=" xảy ra khi `x=1`
`e)-3x^2+5x+10`
`=-3(x^2-5/3x)+10`
`=-3(x^2-5/3x+25/36-25/36)+10`
`=-3(x-5/6)^2+25/12+10`
`=-3(x-5/6)^2+145/12<=145/12`
Dấu "=" xảy ra khi`x=5/6`

a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật

\(b,\dfrac{2x}{7x-21}=\dfrac{2x\left(x+3\right)}{7\left(x-3\right)\left(x+3\right)};\dfrac{x+2}{x^2-9}=\dfrac{7\left(x+2\right)}{7\left(x-3\right)\left(x+3\right)}\\ c,\dfrac{3x}{5x^2-30x}=\dfrac{3}{5\left(x-6\right)}=\dfrac{3\left(x-6\right)}{5\left(x-6\right)^2}\\ \dfrac{x+1}{x^2-12x+36}=\dfrac{5\left(x+1\right)}{5\left(x-6\right)^2}\\ d,\dfrac{2x-1}{5x^2+35x}=\dfrac{\left(2x-1\right)\left(x+7\right)}{5x\left(x+7\right)^2};\dfrac{x-2}{x^2+14x+49}=\dfrac{5x\left(x-2\right)}{5x\left(x+7\right)^2}\)

a: \(A=\left(x+2+2x-5\right)^2=\left(3x-3\right)^2\)
\(=\left(\dfrac{3}{4}-3\right)^2=\left(-\dfrac{9}{4}\right)^2=\dfrac{81}{16}\)


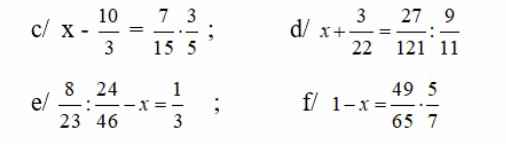




 Ai giải hộ mình bài 18 với! Mình đang cần gấp lắm :(( Cảm ơn trước nha
Ai giải hộ mình bài 18 với! Mình đang cần gấp lắm :(( Cảm ơn trước nha