
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi quãng đg 3 xe chạy lần lượt là a,b,c (km)(a,b,c>0)
Vì vận tốc tỉ lệ với 3;4;5 nên quãng đường tỉ lệ với 5;4;3 \(a:b:c=5:4:3\Rightarrow\dfrac{a}{5}=\dfrac{b}{4}=\dfrac{c}{3}\) và \(a-c=20\left(km\right)\)
Áp dụng t/c dtsbn:
\(\dfrac{a}{5}=\dfrac{b}{4}=\dfrac{c}{3}=\dfrac{a-c}{5-3}=\dfrac{20}{2}=10\\ \Rightarrow\left\{{}\begin{matrix}a=50\\b=40\\c=30\end{matrix}\right.\)
Vậy ...

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
Suy ra: BD=CE
b: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
EC=DB
Do đó:ΔEBC=ΔDCB
Suy ra: \(\widehat{KCB}=\widehat{KBC}\)
hay ΔKBC cân tại K
d: Xét ΔABK và ΔACK có
AB=AC
BK=CK
AK chung
Do đó: ΔABK=ΔACK
Suy ra: \(\widehat{BAK}=\widehat{CAK}\)
hay AK là tia phân giác của góc BAC


Gọi số tiền ba người nhận được lần lượt là x,y,z
Số trang người thứ nhất đánh được là :
16 . 3 = 48 trang
Số trang người thứ hai đánh được là :
12 . 5 = 60 trang
Số trang người thứ 3 đánh được là :
14 . 4 = 56 trang
Vì số tiền nhận được mỗi người dựa vào năng suất làm việc
\(\Rightarrow\frac{a}{48}=\frac{b}{60}=\frac{c}{56}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{a}{48}=\frac{b}{60}=\frac{c}{56}=\frac{a+b+c}{48+60+56}=\frac{410000}{164}=2500\)
Như vậy , \(\hept{\begin{cases}\frac{a}{48}=2500\\\frac{b}{60}=2500\\\frac{c}{56}=2500\end{cases}\Rightarrow}\hept{\begin{cases}a=120000\\b=150000\\c=140000\end{cases}}\)
Vậy : ...


a) Xét ΔNMD và ΔNED có
NM=NE(gt)
\(\widehat{MND}=\widehat{END}\)(ND là tia phân giác của \(\widehat{NME}\))
ND chung
Do đó: ΔNMD=ΔNED(c-g-c)
Suy ra: \(\widehat{NMD}=\widehat{NED}\)(hai góc tương ứng)
mà \(\widehat{NMD}=90^0\)(gt)
nên \(\widehat{NED}=90^0\)
hay DE\(\perp\)NP
b) Ta có: NM=NE(gt)
nên N nằm trên đường trung trực của ME(1)
Ta có: DM=DE(ΔNMD=ΔNED)
nên D nằm trên đường trung trực của ME(2)
Từ (1) và (2) suy ra ND là đường trung trực của ME

\(x^2+4x+y^2-2xy+x^2+4=0\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(x^2+4x+4\right)=0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(x+2\right)^2=0\)
vì \(\left(x-y\right)^2\ge0;\left(x+2\right)^2\ge0\)nên
\(\Rightarrow\orbr{\begin{cases}x+2=0\\x-y=0\end{cases}\Rightarrow\orbr{\begin{cases}x=-2\\y=-2\end{cases}\Rightarrow}x=y=-2}\)

Ta có |5x-5012| = |-5x+5012| >_ -5x +5012.Dấu "=" khi -5x+5012>0
| 5x+300|>_ 5x+300.Dấu "=" khi 5x+300>0
=> |-5x+5012| + |5x+300| >_ -5x+5012 +5x + 300
=> A >_ 5312
Dấu "=" khi -5x+5012>0 => x<5012/5
5x+300> 0 => x>-60
Vậy Min A = 5312 khi -60<x<5012/5



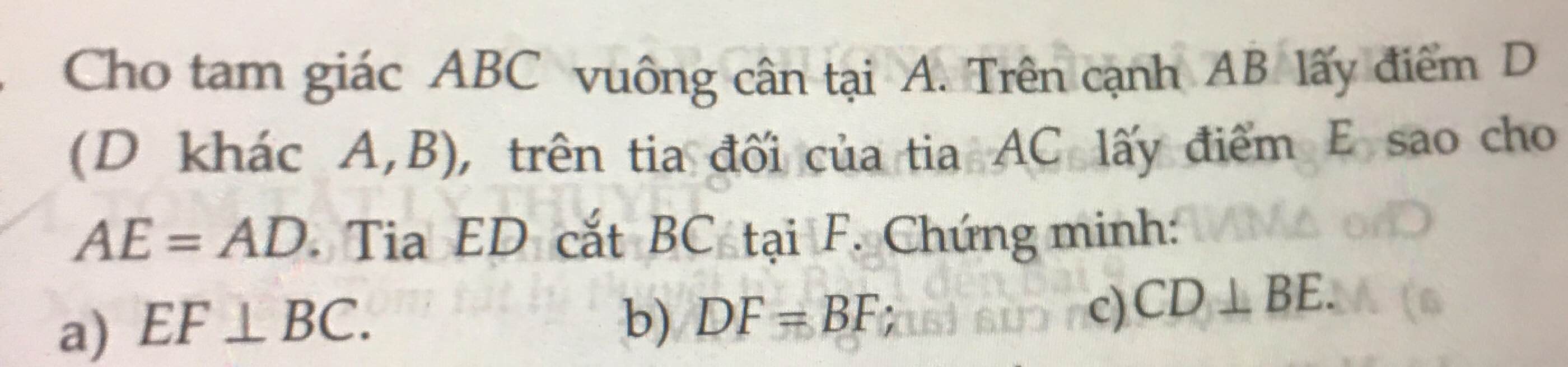

Bài 1:
Vì AD là p/g góc A nên \(\widehat{A_1}=\widehat{A_2}=\dfrac{1}{2}\widehat{BAC}=30^0\)
Mà \(\widehat{A_2}+\widehat{C}+\widehat{D_1}=180^0\Rightarrow\widehat{D_1}=180^0-30^0-40^0=110^0\)
Mà AE//BC nên \(\widehat{EAD}=\widehat{D_1}=110^0\left(so.le.trong\right)\)
Vì DE//AC nên \(\widehat{A_2}=\widehat{D_2}=30^0\left(so.le.trong\right);\widehat{D_3}=\widehat{C}=40^0\left(đồng.vị\right)\)
Vì AE//BC nên \(\widehat{D_3}=\widehat{E}=40^0\)
Vậy các góc tg ADE là \(\widehat{A}=110^0;\widehat{D}=30^0;\widehat{E}=40^0\)
thế còn câu 2, mình chỉ cần câu a,b thôi được ko ??