mầy mới ngu

mk nghĩ các bn không được đăng những câu hỏi k liên quan đến toán thì hơn , ok ! 

chọn Cynthia

Đừng buồn nữa bạn ơi !!!!!!

T_T

chúc các bạn trả lời vu vẻ nha ^^

uk cảm ơn về lời chúc

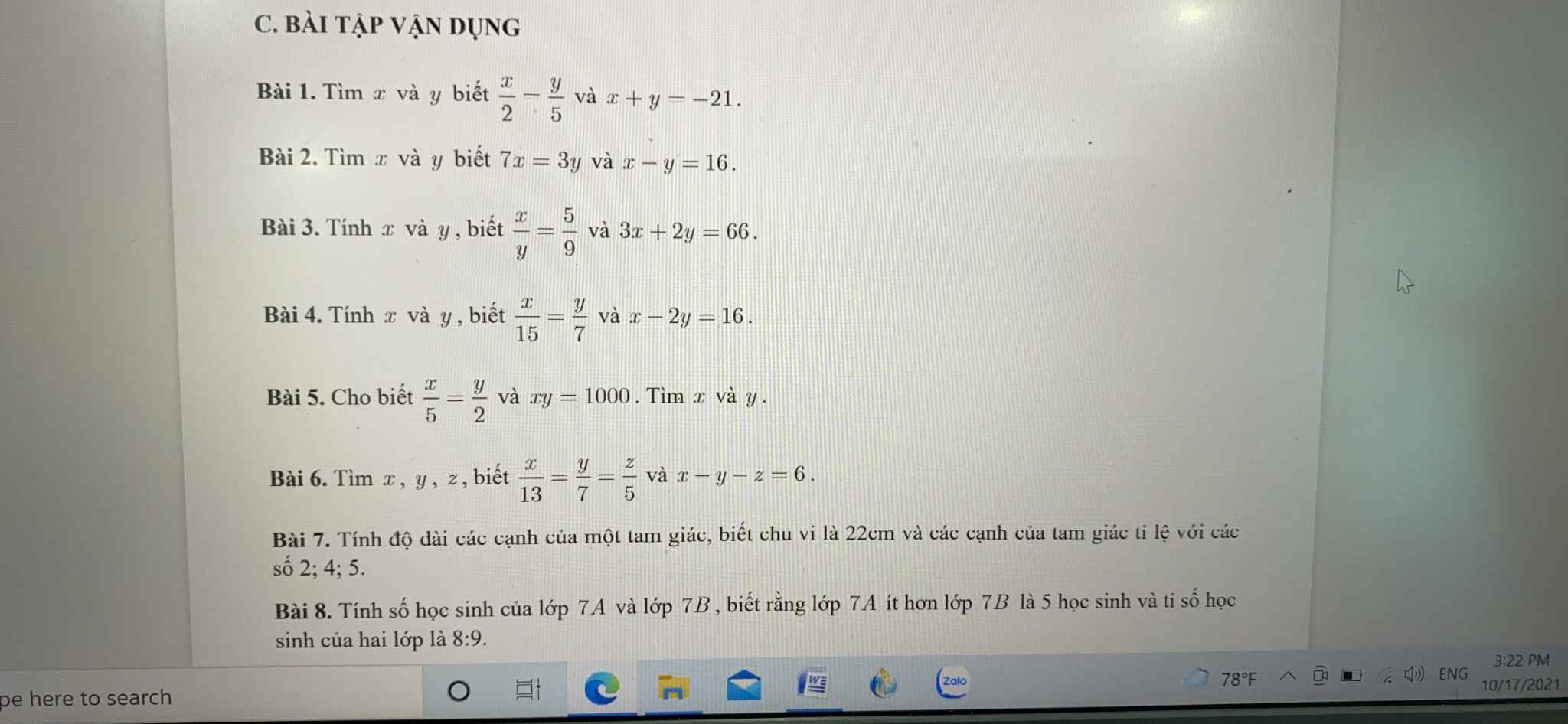
Bài 6: 

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{13}=\dfrac{y}{7}=\dfrac{z}{5}=\dfrac{x-y-z}{13-7-5}=\dfrac{6}{1}=6\)

Do đó: x=78; y=42; z=30

–o0o–

1. Lũy thừa với số mũ tự nhiên :

Định nghĩa :

Lũy thừa bậc n của số hữu tỉ x, kí hiệu xⁿ, là tích của n thừa số x (n là số tự nhiên lớn hơn 1).

Công thức :

xⁿ = x.x…x (n thừa số).

x  Q, n  N, n > 1

ta có : a, b  Z, b ≠ 0 :

Quy ước :

• x¹ = x
• x⁰ = 1 (x ≠ 0)

2. Các công thức tính : x là số hữu tỉ.

Tích các lũy thừa cùng cơ số :

x^m . xⁿ = x^{m + n}

thương các lũy thừa cùng cơ số:

x^m : xⁿ = x^{m – n}

lũy thừa của lũy thừa :

(x^m)ⁿ = x^{m . n}

lũy thừa của một tích :

(x . y)ⁿ = xⁿ . yⁿ

lũy thừa của một thương :

(x : y)ⁿ = xⁿ : yⁿ

Lũy thừa của không và một[sửa | sửa mã nguồn]

{\displaystyle 0^{n}=0\,}.

{\displaystyle 1^{n}=1\,}.

Lũy thừa với số mũ nguyên dương[sửa | sửa mã nguồn]

Trong trường hợp b = n là số nguyên dương, lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a:

{\displaystyle a^{n}=\underbrace {a\times a\cdots \times a} _{n}}

Các tính chất quan trong nhất của lũy thừa với số mũ nguyên dương m, n là

{\displaystyle a^{m+n}=a^{m}\times a^{n}}

{\displaystyle a^{m-n}={\frac {a^{m}}{a^{n}}}} với mọi a ≠ 0

{\displaystyle (a^{m})^{n}=a^{mn}}

{\displaystyle a^{m^{n}}=a^{(m^{n})}}

{\displaystyle (a\times b)^{n}=a^{n}\times b^{n}}

{\displaystyle ({\frac {a}{b}})^{n}={\frac {a^{n}}{b^{n}}}}

Đặc biệt, ta có:

{\displaystyle a^{1}=a}

Trong khi các phép cộng và phép nhân có tính chất giao hoán, phép tính lũy thừa không có tính giao hoán.

Tương tự các phép cộng và nhân có tính kết hợp, còn phép tính lũy thừa thì không.. Khi không có dấu ngoặc, thứ tự tính của các lũy thừa là từ trên xuống, chứ không phải là từ dưới lên:

{\displaystyle a^{b^{c}}=a^{(b^{c})}\neq (a^{b})^{c}=a^{(b\cdot c)}=a^{b\cdot c}}

Lũy thừa với số mũ 0[sửa | sửa mã nguồn]

Lũy thừa với số mũ 0 của số a khác không được quy ước bằng 1.

{\displaystyle a^{0}=1}

Chứng minh:

{\displaystyle 1={\frac {a^{n}}{a^{n}}}=a^{n-n}=a^{0}}

Em học lớp 6 nên chỉ biết về lũy thừa. Công thức về căn số em chịu

chắc chắn 100 % đó cá nhà khoa học đã cm đc rồi mà

người ngoài hành tinh là có thật, nhưng đôi khi đó lại là 1 số chí tưởng tượng của con người

\(\frac{3}{1^22^2}+\frac{5}{2^23^2}+\frac{7}{3^24^2}+....+\frac{19}{9^210^2}< 1\)

\(A=\frac{3}{1^22^2}+\frac{5}{2^23^2}+\frac{7}{3^24^2}+....+\frac{19}{9^210^2}\)

A=\(\frac{1}{1}-\frac{1}{2^2}+\frac{1}{2^2}-\frac{1}{3^2}+\frac{1}{3^2}-\frac{1}{4^2}+...+\frac{1}{9^2}-\frac{1}{10^2}\)

A=\(1-\frac{1}{10^2}\)

A=\(1-\frac{1}{100}\)

A=\(\frac{99}{100}< 1\)

\(\Rightarrow\frac{3}{1^22^2}+\frac{5}{2^23^2}+\frac{7}{3^24^2}+....+\frac{19}{9^210^2}< 1\)