a) (C) có tâm I và đi qua M nên bán kính R = IM

Ta có: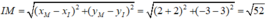 

Vậy đường tròn (C) : (x + 2)2 + (y – 3)2 = 52.

b) (C) tiếp xúc với (Δ) : x – 2y + 7 = 0

⇒ d(I; Δ) = R

Mà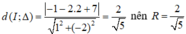 

Vậy đường tròn (C) :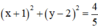 

c) (C) có đường kính AB nên (C) có :

+ tâm I là trung điểm của AB

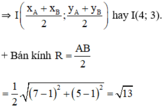
Vậy đường tròn (C) : (x – 4)2 + (y – 3)2 = 13.

a) Phương trình đường tròn \(\left( C \right)\) là: \({\left( {x + 2} \right)^2} + {\left( {y - 5} \right)^2} = 49\).

b) Bán kính đường tròn là: \(R = IA = \sqrt {{{\left( { - 2 - 1} \right)}^2} + {{\left( {2 - \left( { - 2} \right)} \right)}^2}}  = 5\)

Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 25\)

c) Gọi \(I\left( {a;b} \right)\) là trung điểm AB. Vậy tọa độ điểm I là: \(I\left( { - 2;1} \right)\)

Bán kính đường tròn là: \[R = IA = \sqrt {{{\left( { - 1 + 2} \right)}^2} + {{\left( { - 3 - 1} \right)}^2}}  = \sqrt {17} \]

Phương trình đường tròn là: \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} = 17\)

d) Bán kính đường tròn là: \(R = \frac{{\left| {1 + 2.3 + 3} \right|}}{{\sqrt {{1^2} + {2^2}} }} = 2\sqrt 5 \)

Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 20\)

Gọi I là trung điểm AB \(\Rightarrow I\left(2;-3\right)\Rightarrow\overrightarrow{IA}=\left(1;2\right)\Rightarrow IA=\sqrt{1^2+2^2}=\sqrt{5}\)

Đường tròn đường kính AB nhận I là tâm và có bán kính R=IA nên có pt:

\(\left(x-2\right)^2+\left(y+3\right)^2=5\)

Tâm I của đường tròn là trung điểm của AB nên I( 1;3) .

Bán kính

Vậy phương trình đường tròn là:

(x-1) ²+ (y-3) ²= 32 hay . x²+y²-2x- 6y- 22 = 0

Chọn B.

Đáp án B

Tâm I của đường tròn là trung điểm AB nên I( 1; 3) .

Bán kính

Vậy phương trình đường tròn là: (x-1)²+ (y-3) ²= 32

Hay x²+ y²- 2x- 6y - 22= 0.

Chọn B.

Sửa:

Tâm `I` của đtr `(C)` là trung điểm của `AB`

`=>I(2;-3)`

Ta có: `R=IA=\sqrt{(3-2)^2+(-1+3)^2}=\sqrt{5}`

`=>` Ptr đtr `(C)` có tâm `I(2;-3)` và `R=\sqrt{5}` là:

         `(x-2)^2+(y+3)^2=5`

\(I\left(2;-3\right)\)

\(R=\dfrac{\sqrt{\left(3-1\right)^2+\left(1-5\right)^2}}{2}=\sqrt{5}\)

--> pt đường tròn là \(\left(x-2\right)^2+\left(x+3\right)^2=5\)

a) Phương trình đường tròn là: \({\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} = 81\)

b) Bán kính đường tròn là: \(R = IM = \sqrt {{{\left( {4 - 5} \right)}^2} + {{\left( { - 1 + 2} \right)}^2}}  = \sqrt 2 \)

Phương trình đường tròn là: \({\left( {x - 5} \right)^2} + {\left( {y + 2} \right)^2} = 2\)

c) Bán kính đường tròn là: \(R = \frac{{\left| {5.1 - 12.\left( { - 1} \right) - 1} \right|}}{{\sqrt {{5^2} + {{\left( { - 12} \right)}^2}} }} = \frac{{16}}{{13}}\)

Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} = {\left( {\frac{{16}}{{13}}} \right)^2}\)

d) Gọi \(I\left( {a;b} \right)\) là trung điểm AB. Vậy tọa độ điểm I là: \(I\left( {1;1} \right)\)

Bán kính đường tròn là: \(R = IA = \sqrt {{{\left( {3 - 1} \right)}^2} + {{\left( { - 4 - 1} \right)}^2}}  = \sqrt {29} \)

Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 29\)

e) Giả sử  tâm đường tròn là điểm \(I\left( {a;b} \right)\). Ta có: \(IA = IB = IC \Leftrightarrow I{A^2} = I{B^2} = I{C^2}\)

Vì \(I{A^2} = I{B^2},I{B^2} = I{C^2}\) nên: \(\left\{ \begin{array}{l}{\left( {1 - a} \right)^2} + {\left( {1 - b} \right)^2} = {\left( {3 - a} \right)^2} + {\left( {1 - b} \right)^2}\\{\left( {3 - a} \right)^2} + {\left( {1 - b} \right)^2} = {\left( {0 - a} \right)^2} + {\left( {4 - b} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 3\end{array} \right.\)  b

Vậy \(I\left( {2;3} \right)\) và \(R = IA = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2}}  = \sqrt 5 \)

Vậy phương trình đường tròn đi qua 3 điểm A,B, C là: \({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 5\)

Tọa độ trung điểm I của AB là: x =    − 2 + 4 2 = 1 y =    1 + ​ 1 2 = 1  

Đường tròn có tâm I(1; 1) là trung điểm của AB và có bán kính R ​ =    I A ​ =    ( − 2 − 1 ) 2 + ​ ( 1   − 1 ) 2 = 3 nên phương trình của đường tròn là:

  x − 1 2 + y − 1 2 = 9   ⇔ x 2 + y 2 − 2 x − 2 y − 7 = 0

ĐÁP ÁN C