
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Do MN là đường trung bình tam giác ABC \(\Rightarrow MN||AB\) mà \(AB||CD\Rightarrow MN||CD\)
MN và (ABCD) không có điểm chung \(\Rightarrow MN||\left(ABCD\right)\)
MN và (SCD) không có điểm chung \(\Rightarrow MN||\left(SCD\right)\)
MN nằm trên (SAB) nên MN không song song (SAB)
Vậy MN song song với cả (ABCD) và (SCD)

\(L=\lim\limits_{x\rightarrow+\infty}\left(2x^2-\sqrt{x^2-x}.\sqrt[3]{8x^3+12x^2-3x}\right)\)
Đặt \(f\left(x\right)=2x^2-\sqrt{x^2-x}.\sqrt[3]{8x^3+12x^2-3x}\)
Ta có:
\(2.f\left(x\right)=4x^2-\sqrt{4x^2-4x}.\sqrt[3]{8x^3+12x^2-3x}\)
\(=1+\left(4x^2-1\right)-\sqrt{4x^2-4x}.\sqrt[3]{8x^3+12x^2-3x}\)
\(=1+\left(2x-1\right)\left(2x+1-\sqrt[3]{8x^3+12x^2-3x}\right)+\left(2x-1-\sqrt{4x^2-4x}\right).\sqrt[3]{8x^3+12x^2-3x}\)
Đặt \(A\left(x\right)=\left(2x-1\right)\left(2x+1-\sqrt[3]{8x^3+12x^2-3x}\right)\)
\(B\left(x\right)=\left(2x-1-\sqrt{4x^2-4x}\right).\sqrt[3]{8x^3+12x^2-3x}\)
\(A\left(x\right)=\left(2x-1\right)\left(2x+1-\sqrt[3]{8x^3+12x^2-3x}\right)\)
\(=\dfrac{\left(2x-1\right)\left(8x^3+12x^2+6x+1-8x^3-12x^2+3x\right)}{\left(2x+1\right)^2+\sqrt[3]{\left(8x^3+12x^2-3x\right)^2}+\left(2x+1\right)\sqrt[3]{8x^3+12x^2-3x}}\)
\(=\dfrac{\left(2x-1\right)\left(9x+1\right)}{\left(2x+1\right)^2+\sqrt[3]{\left(8x^3+12x^2-3x\right)^2}+\left(2x+1\right)\sqrt[3]{8x^3+12x^2-3x}}\)
\(\Rightarrow\lim\limits_{x\rightarrow+\infty}A\left(x\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2-\dfrac{1}{x}\right)\left(9+\dfrac{1}{x}\right)}{\left(2+\dfrac{1}{x}\right)^2+\sqrt[3]{\left(8+\dfrac{12}{x}-\dfrac{3}{x^2}\right)^2}+\left(2+\dfrac{1}{x}\right)\sqrt[3]{8+\dfrac{12}{x}-\dfrac{3}{x^2}}}\)
\(=\dfrac{2.9}{2^2+4+2.2}\)
\(=\dfrac{3}{2}\)
\(B\left(x\right)=\left(2x-1-\sqrt{4x^2-4x}\right).\sqrt[3]{8x^3+12x^2-3x}\)
\(=\dfrac{\left(4x^2-4x+1-4x^2+4x\right).\sqrt[3]{8x^3+12x^2-3x}}{2x-1+\sqrt{4x^2-4x}}\)
\(=\dfrac{\sqrt[3]{8x^3+12x^2-3x}}{2x-1+\sqrt{4x^2-4x}}\)
\(\Rightarrow\lim\limits_{x\rightarrow+\infty}B\left(x\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt[3]{8+\dfrac{12}{x}-\dfrac{3}{x^2}}}{2-\dfrac{1}{x}+\sqrt{4-\dfrac{4}{x}}}\)
\(=\dfrac{2}{2+2}\)
\(=\dfrac{1}{2}\)
\(\Rightarrow2L=\lim\limits_{x\rightarrow+\infty}\left[2f\left(x\right)\right]\)
\(=\lim\limits_{x\rightarrow+\infty}\left[1+A\left(x\right)+B\left(x\right)\right]\)
\(=1+\lim\limits_{x\rightarrow+\infty}A\left(x\right)+\lim\limits_{x\rightarrow+\infty}B\left(x\right)\)
\(=1+\dfrac{3}{2}+\dfrac{1}{2}\)
\(=3\)
\(\Rightarrow L=\dfrac{3}{2}\)


\(y=\dfrac{sinx-cosx}{sinx+cosx}\Rightarrow y'=\dfrac{\left(sinx-cosx\right)'.\left(sinx+cosx\right)-\left(sinx+cosx\right)'.\left(sinx-cosx\right)}{\left(sinx+cosx\right)^2}\)
Dễ thấy : \(\left(sinx-cosx\right)'=cosx+sinx\)
\(\left(sinx+cosx\right)'=cosx-sinx\)
Suy ra : \(y'=\dfrac{\left(sinx+cosx\right)^2+\left(sinx-cosx\right)^2}{\left(sinx+cosx\right)^2}=\dfrac{2}{\left(sinx+cosx\right)^2}\)

\(\Leftrightarrow2cos4x\left(cos2x-sin2x\right)=0\)
\(\Leftrightarrow cos4x=0\) (do \(cos4x=cos^22x-sin^22x\) đã bao hàm \(cos2x-sin2x\))
\(\Rightarrow4x=\dfrac{\pi}{2}+k\pi\)
\(\Rightarrow x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\)

\(lim\left(\sqrt[3]{n^3+4}-\sqrt[3]{n^3-1}\right)\)
\(=lim\left(\sqrt[3]{1+\dfrac{4}{n^3}}-\sqrt[3]{1-\dfrac{1}{n^3}}\right)=\sqrt[3]{1}-\sqrt[3]{1}=0\)

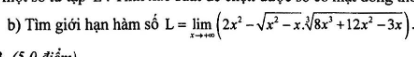


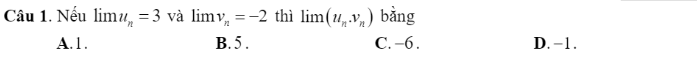



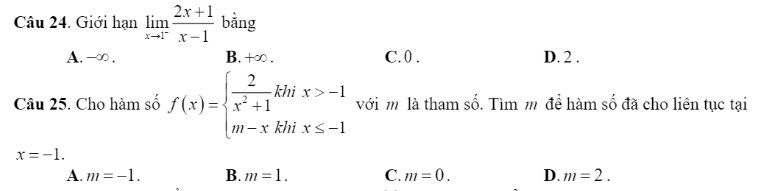

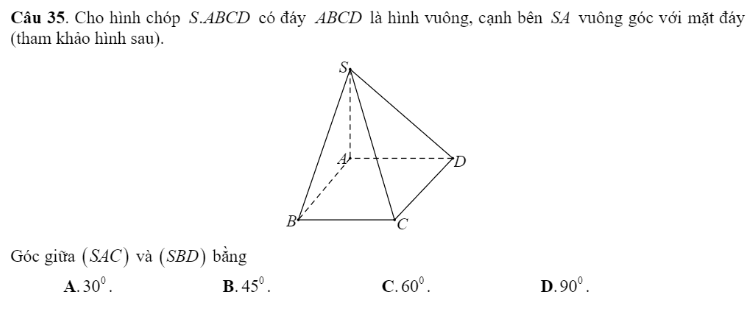

Chọn B