
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a. Ta có \(\sqrt{\dfrac{2}{x^2}}=\dfrac{\sqrt{2}}{\left|x\right|}=\dfrac{\sqrt{2}}{x}\) ,để biểu thức có nghĩa thì \(x>0\)
b. Để biểu thức \(\sqrt{\dfrac{-3}{3x+5}}\) có nghĩa thì \(\dfrac{-3}{3x+5}\ge0\)
mà \(-3< 0\Rightarrow3x+5< 0\) \(\Rightarrow x< \dfrac{-5}{3}\)
Bài 2:
a. \(\dfrac{2+\sqrt{2}}{1+\sqrt{2}}=\dfrac{\left(2+\sqrt{2}\right)\left(1-\sqrt{2}\right)}{1-2}=\dfrac{-\sqrt{2}}{-1}=\sqrt{2}\)
b. \(\left(\sqrt{28}-2\sqrt{14}+\sqrt{7}\right)\sqrt{7}+7\sqrt{8}\)
\(=14-14\sqrt{2}+7+14\sqrt{2}\)
\(=21\)
c. \(\left(\sqrt{14}-3\sqrt{2}\right)^2+6\sqrt{28}\)
\(=14-6\sqrt{28}+18+6\sqrt{28}\)
\(=32\)

`a)(\sqrt{14}-3\sqrt{2})^2+6\sqrt{28}`
`=14-12\sqrt{7}+18+12\sqrt{7}=32`
`b)2\sqrt{20}-3\sqrt{20}+\sqrt{125}`
`=4\sqrt{5}-6\sqrt{5}+5\sqrt{5}`
`=3\sqrt{5}`.
a) \(\left(\sqrt{14}-3\sqrt{2}\right)^2-6\sqrt{28}\)
\(=\left(\sqrt{14}\right)^2-2\cdot\sqrt{14}\cdot3\sqrt{2}+\left(3\sqrt{2}\right)^2+6\sqrt{28}\)
\(=14-6\sqrt{28}+18+6\sqrt{28}\)
\(=14+18\)
\(=32\)
b) \(2\sqrt{20}-3\sqrt{20}+\sqrt{125}\)
\(=2\cdot2\sqrt{5}-3\cdot2\sqrt{5}+5\sqrt{5}\)
\(=4\sqrt{5}-6\sqrt{5}+5\sqrt{5}\)
\(=3\sqrt{5}\)

Ta có: \(\left(\sqrt{14}-3\sqrt{2}\right)^2+6\sqrt{28}\)
\(=14+18-6\sqrt{28}+6\sqrt{28}\)
=32

\(a.\dfrac{2}{4-3\sqrt{2}}-\dfrac{2}{4+3\sqrt{2}}=\dfrac{2\left(4+3\sqrt{2}\right)-2\left(4-3\sqrt{2}\right)}{\left(4-3\sqrt{2}\right)\left(4+3\sqrt{2}\right)}=\dfrac{8+6\sqrt{2}-8+6\sqrt{2}}{16-18}=\dfrac{12\sqrt{2}}{-2}=-6\sqrt{2}\)\(b.\dfrac{2}{1+\sqrt{2}}+\dfrac{2}{1-\sqrt{2}}=\dfrac{2\left(1-\sqrt{2}\right)+2\left(1+\sqrt{2}\right)}{\left(1+\sqrt{2}\right)\left(1-\sqrt{2}\right)}=\dfrac{2-2\sqrt{2}+2+2\sqrt{2}}{1-2}=-4\)\(c.\left(\sqrt{14}-3\sqrt{2}\right)^2+6\sqrt{28}=14-12\sqrt{7}+18+12\sqrt{7}=14+18=32\)\(d.\left(\sqrt{28}-2\sqrt{14}+\sqrt{7}\right).\sqrt{7}+7\sqrt{8}=14-14\sqrt{2}+7+14\sqrt{2}=14+7=21\)\(e.\left(\sqrt{6}-\sqrt{5}\right)^2-2\sqrt{120}=6-2\sqrt{30}+5-4\sqrt{30}=11-6\sqrt{30}\)

Thêm câu này hộ tớ nx nhé !
e) \(\left(\sqrt{8}-3\sqrt{2}+\sqrt{10}\right).\left(\sqrt{2}-3\sqrt{0.4}\right)\)
\(a,\left(\frac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\frac{\sqrt{216}}{3}\right)\cdot\frac{1}{\sqrt{6}}\)
\(=\left(\frac{\sqrt{12}-\sqrt{6}}{2\left(\sqrt{2}-1\right)}-\frac{6\sqrt{6}}{3}\right)\cdot\frac{1}{\sqrt{6}}\)
\(=\left(\frac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}-2\sqrt{6}\right)\cdot\frac{1}{\sqrt{6}}\)
\(=\left(\frac{\sqrt{6}}{2}-\frac{4\sqrt{6}}{2}\right)\cdot\frac{1}{\sqrt{6}}\)
\(=\frac{\sqrt{6}-4\sqrt{6}}{2}\cdot\frac{1}{\sqrt{6}}\)
\(=\frac{-3\sqrt{6}}{2}\cdot\frac{1}{\sqrt{6}}\)
\(=-\frac{3}{2}\)

g, h. Câu hỏi của Nữ hoàng sến súa là ta - Toán lớp 9 - Học toán với OnlineMath

\(a,\left(\sqrt{14}-3\sqrt{2}\right)^2+6\sqrt{28}\)
\(=14-12\sqrt{7}+18+12\sqrt{7}\)
\(=32\)
\(b,\left(3\sqrt{5}+2\sqrt{3}\right).\sqrt{5}-\sqrt{60}\)
\(=15+2\sqrt{15}-2\sqrt{15}\)
\(=15\)
Đúng thì ủng hộ nha ...
Kết bạn với mình .. ;) ;)
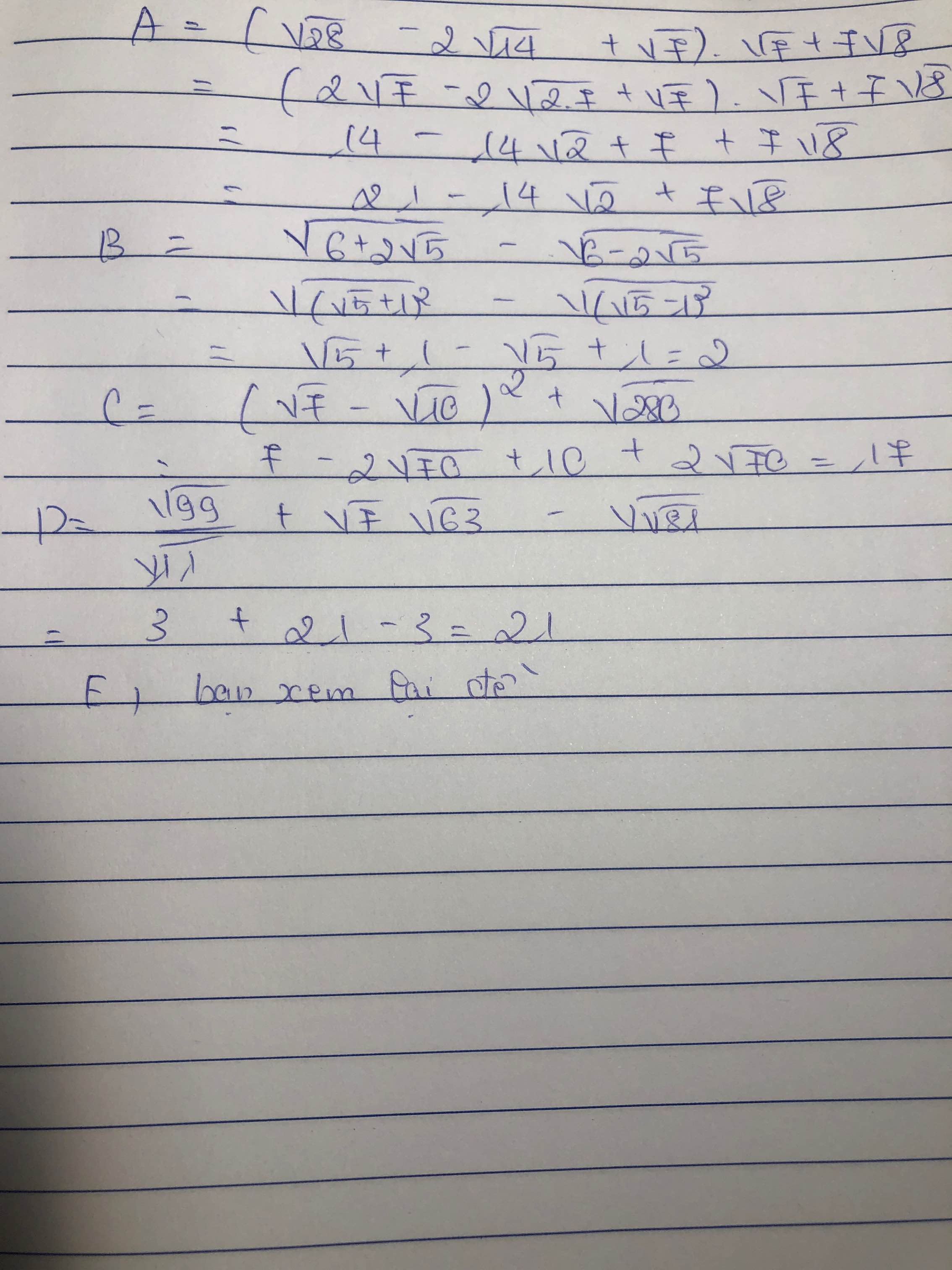
\(\left(\sqrt{14}-3\sqrt{2}\right)^3+6\sqrt{28}\)
\(=\left(\sqrt{14}\right)^2-2\cdot3\sqrt{2}\cdot\sqrt{14}+\left(3\sqrt{2}\right)^2+6\cdot2\sqrt{7}\)
\(=14-6\sqrt{28}+9\cdot2+12\sqrt{7}\)
\(=14-6\cdot2\sqrt{7}+18+12\sqrt{7}\)
\(=\left(14+18\right)+\left(12\sqrt{7}-12\sqrt{7}\right)\)
\(=32\)