Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

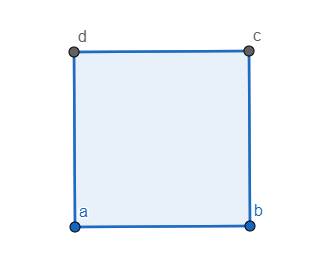
Xét 1 mặt bất kì của khối lập phương như hình vẽ và gọi 4 số ở đỉnh là a, b, c, d. Khi đó do \(a+b+c,b+c+d,c+d+a,d+a+b\ge10\) nên \(3\left(a+b+c+d\right)\ge40\) \(\Rightarrow a+b+c+d\ge14\)
Làm tương tự cho 4 mặt còn lại, ta đều được tổng của 4 số trên mỗi mặt đều không nhỏ hơn 14.
Nhưng trong một mặt, sẽ có mặt có chứa đỉnh mang số 8. Khi đó 3 đỉnh còn lại bắt buộc là 1, 2, 3, mà \(1+2+3< 10\), vô lí. Lập luận tương tự cho trường hợp GTNN là 15, 16, 17. Nếu GTNN là 18, ta chỉ ra 1 trường hợp dấu "=" xảy ra:
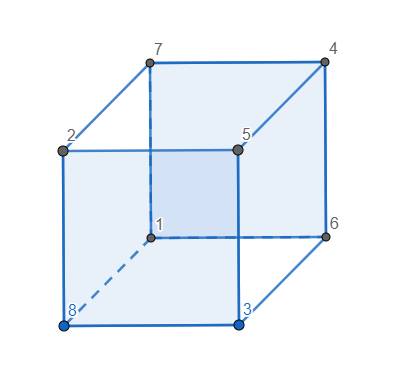
Vậy GTNN của 4 số trong cùng 1 mặt là 18.

(IMO 2016 mà đưa vô đây chi?)
Dễ thấy nếu xoá ít hơn 2016 nhân tử thì không được, vì khi đó ở hai vế sẽ có nhân tử chung.
Ta sẽ CM có thể xoá đúng 2016 nhân tử, bằng cách:
\(\left(x-1\right)\left(x-4\right)\left(x-5\right)\left(x-8\right)...=\left(x-2\right)\left(x-3\right)\left(x-6\right)\left(x-7\right)...\)
Tự CM pt này vô nghiệm nha bạn.

Trên mặt phẳng cho n > = điểm sao cho khoảng cách giữa 2 điểm bất kì đôi một khác nhau. Người ta nối mỗi điểm với điểm gần nhất.
CMR qua mỗi điểm co không quá 5 đoạn thẳng
36 số nha bạn
tk mk nha
mk trả lời nhầm ,sorry