a) Có \(\widehat{OAM}=90^0\) => Tam giác \(OAM\) nội tiếp đường tròn đường kính OM 

=> O,A,M cùng thuộc đường tròn đường kính OM (*)

Có \(\widehat{OBM}=90^0\) => Tam giác \(OBM\) nội tiếp đường tròn đường kính OM 

=> O,B,M cùng thuộc đường tròn đường kính OM (2*)

Do N là trung điểm của PQ => \(ON\perp PQ\)( Vì trong một đt, đường kính đi qua trung điểm của một dây ko đi qua tâm thì vuông góc với dây ấy)

=> \(\widehat{ONM}=90^0\) => Tam giác \(ONM\) nội tiếp đường tròn đường kính OM 

=> O,N,M cùng thuộc đt đường kính OM (3*)

Từ (*) (2*) (3*) => O,M,N,A,B cùng thuộc đt đk OM hay đt bán kính \(\dfrac{OM}{2}\)

b) Có AM//PS (cùng vuông góc với OA)

Gọi E là gđ của PS với (O) => \(sđ\stackrel\frown{AE}=sđ\stackrel\frown{AP}\)

Có \(\widehat{PRB}=\dfrac{1}{2}\left(sđ\stackrel\frown{AE}+sđ\stackrel\frown{PB}\right)\)\(=\dfrac{1}{2}\left(sđ\stackrel\frown{AP}+sđ\stackrel\frown{PB}\right)=\dfrac{1}{2}sđ\stackrel\frown{AB}\)

=> \(\widehat{PRB}=\widehat{MAB}=\dfrac{1}{2}sđ\stackrel\frown{AB}\)

Có BNAM nội tiếp => \(\widehat{MAB}=\widehat{MNB}\)

\(\Rightarrow\widehat{PRB}=\widehat{MNP}\) => PRNB nội tiếp

\(\Rightarrow\widehat{BRN}=\widehat{BPN}\) mà \(\widehat{BPN}=\widehat{BAQ}=\dfrac{1}{2}sđ\stackrel\frown{BQ}\)

\(\Rightarrow\widehat{BRN}=\widehat{BAQ}\) => RN//AQ hay RN // SQ mà N la trung điểm của PQ

=> RN là đường TB của tam giác PSQ

=> R là trung điểm của PS <=> PR=RS

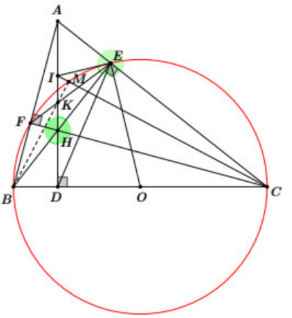
Xét tứ giác AEDB có: \(\widehat{AEB} = \widehat{ADB} = 90^o \)

⇒ Tứ giác AEDB nội tiếp (2 đỉnh E và D kề nhau cùng nhìn AB dưới 1 cặp góc bằng nhau)

⇒ \(\widehat{EAD} = \widehat{EBD} \) (cùng chắn \(\stackrel\frown{\text{ED}}\))

Xét ΔADC và ΔHDB có:

\(\widehat{ADC} = \widehat{HDB} = 90^o\)

\(\widehat{CAD} = \widehat{HBD} \)   (cmt)

⇒ ΔADC ∼ ΔBDH (g-g)

giúp mik vs

a: \(=2\sqrt{3}-\sqrt{5}-2\sqrt{5}-2\sqrt{3}+3\left(\sqrt{5}-1\right)\)

\(=-3\sqrt{5}+3\sqrt{5}-3\)

=-3

c. \(\left(x+2\right)^4-6\left(x+2\right)^2+5=0\)

\(\Leftrightarrow\left(x+2\right)^4-\left(x+2\right)^2-5\left(x+2\right)^2+5=0\)

\(\Leftrightarrow\left(x+2\right)^2\left[\left(x+2\right)^2-1\right]-5\left[\left(x+2\right)^2-1\right]=0\)

\(\Leftrightarrow\left[\left(x+2\right)^2-1\right]\left[\left(x+2\right)^2-5\right]=0\)

\(\Leftrightarrow\left(x+3\right)\left(x+1\right)\left(x+2+\sqrt{5}\right)\left(x+2-\sqrt{5}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x+1=0\\x+2+\sqrt{5}=0\\x+2-\sqrt{5}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-1\\x=-\sqrt{5}-2\\x=\sqrt{5}-2\end{matrix}\right.\)

Vậy: Phương trình có tập nghiệm \(S=\left\{-3;-1;-\sqrt{5}-2;\sqrt{5}-2\right\}\)

lm cho em câu 4 nữa đc ko

Tui có cách khác đây, góp vui thôi thi đừng xài (bí lắm xài cx dc)

Dự đoán dấu "=" xảy khi \(x=y=z=1\) tính được \(P=3\)

Vậy cần chứng minh đó là GTNN của P

Thật vậy, tức là cần chứng minh 

\(P=\frac{x+1}{1+y^2}+\frac{y+1}{1+z^2}+\frac{z+1}{1+x^2}\ge3\)

\(\Leftrightarrow\frac{3+3x}{9+9y^2}+\frac{3+3y}{9+9z^2}+\frac{3+3z}{9+9x^2}\ge1\)

\(\LeftrightarrowΣ\frac{4x+y+z}{\left(x+y+z\right)^2+9y^2}\ge\frac{3}{x+y+z}\)

\(\LeftrightarrowΣ\left(7x^6+30x^5y+21x^5z-6x^4y^2+57x^4z^2+14x^3y^3+75x^4yz-6x^3y^2z+66x^3z^2y-258x^2y^2z\right)\ge0\)

BĐT cuối đúng vì \(Σx^6\geΣx^4y^2\) theo BĐT Rearrangement còn lại đúng theo AM-GM

P/s:dưới chân mỗi Σ bn ghi chữ "cyc" hộ mk nhé

Hướng giải nè: 

P/s: đây là cách giải của bản thân mik nên chưa bt nó tối ưu chưa

\(\frac{x+1}{1+y^2}=\left(x+1\right)-\frac{y^2.\left(x+1\right)}{1+y^2}\ge\left(x+1\right)-\frac{y.\left(x+1\right)}{2}=x-\frac{y}{2}+1-\frac{xy}{2}\)

bạn lm tương tự r cộng vào,,đánh giá nốt là ok

dễ heo tự giải đi

câu a th mà tuấn 

a)\(đkx\ge1,x\ne-1\)

\(\sqrt{\dfrac{x-1}{x+1}}=2\)

\(\Leftrightarrow\dfrac{x-1}{x+1}=4\)

\(\Leftrightarrow x-1=4x-4\)

\(\Leftrightarrow x=1\)(nhận)

Vậy S=\(\left\{1\right\}\)

c)đk\(25x^2-10x+1=\) \(\left(5x-1\right)^2\ge0\Leftrightarrow x\ge\dfrac{1}{5}\)

\(\sqrt{25x^2-10x+1}+2x=1\)

\(\Leftrightarrow\sqrt{\left(5x-1\right)^2}+2x=1\)

\(\Leftrightarrow5x-1+2x=1\)

\(\Leftrightarrow x=\dfrac{2}{7}\)(nhận)

Vậy S=\(\left\{\dfrac{2}{7}\right\}\)

c: Ta có: \(\sqrt{25x^2-10x+1}+2x=1\)

\(\Leftrightarrow\left|5x-1\right|=1-2x\)

\(\Leftrightarrow\left[{}\begin{matrix}5x-1=1-2x\left(x\ge\dfrac{1}{5}\right)\\5x-1=2x-1\left(x< \dfrac{1}{5}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{7}\left(nhận\right)\\x=0\left(nhận\right)\end{matrix}\right.\)