

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án : A
Để lựa chọn được hai ban thỏa mãn yêu cầu, ta chia làm hai công đoạn.
Công đoạn 1: Chọn một học sinh giỏi nữ, có 9 cách thực hiện.
Công đoạn 2. Chọn một học sinh giỏi nam, có 7 cách thực hiện.
Vậy theo quy tắc nhân, sẽ có 9.7=63 cách lựa chọn.

Đáp án D
Số phần tử không gian mẫu là: C 40 4 = 91390 .
Số cách chọn 4 học sinh có cả học sinh xếp loại giỏi, khá, trung bình là:
C 10 2 . C 20 1 . C 10 1 + C 10 1 . C 20 2 . C 10 1 + C 10 1 . C 20 1 . C 10 2 = 37000
Số cách chọn 4 học sinh nam có cả học sinh xếp loại giỏi, khá, trung bình là:
C 5 2 . C 9 1 . C 6 1 + C 5 1 . C 9 2 . C 6 1 + C 5 1 . C 9 1 . C 6 2 = 2295
Số cách chọn 4 học sinh nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
C 5 2 . C 11 1 . C 4 1 + C 5 1 . C 11 2 . C 4 1 + C 5 1 . C 11 1 . C 4 2 = 1870
Số cách chọn 4 học sinh có cả nam, nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
37000 - 2295 - 1870 = 32835
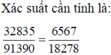

Đáp án : D
Ta cần thực hiện 2 công việc:
Chọn một học sinh nam: có 20 cách chọn.
Chọn một học sinh nữ: có 22 cách chọn.
Theo quy tắc nhân: số cách chọn là 20.22=440 cách chọn.

a) Nếu trong \(5\) học sinh phải có ít nhất \(2\) học sinh nữ và \(2\) học sinh nam thì có \(2\) trường hợp :
\(2\) nam \(3\) nữ, có : \(C^2_{10}.C^3_{10}\) cách:
\(3\) nam và \(2\) nữ, có : \(C^3_{10}.C^2_{10}\) cách:
Vậy tất cả có : \(2.C^2_{10}.C^3_{10}=10800\) cách.
b) Nếu trong \(5\) học sinh phải có ít nhất \(1\) học sinh nữ và \(1\) học sinh nam thì có 4 trường hợp :
\(1\) nam và \(4\) nữ, có: \(C^1_{10}.C^4_{10}\) cách.
\(2\) nam và \(3\) , có : \(C^2_{10}.C^3_{10}\) cách.
Còn lại bn tự lm nha, mỏi tay quá

Đáp án B
Phương pháp giải: Áp dụng các quy tắc đếm cơ bản
Lời giải:
Chọn 2 học sinh trong 20 học sinh có C 20 2 = 190 ⇒ n ( Ω ) = 190 .
Gọi X là biến cố 2 học sinh được chọn trong đó có cả nam và nữ
Chọn 1 học sinh nam trong 8 nam có 8 cách, chọn 1 học sinh nữ trong 12 nữ có 12 cách.
Suy ra số kết quả thuận lợi cho biến cố X là n(X) = 8.12 = 96.
Vậy P = n ( X ) N ( Ω ) = 48 95 .

Trường hợp 1: Chọn 3 nữ, 2 nam ⇒ có ![]() cách chọn
cách chọn
Trường hợp 2: Chọn 4 nữ, 1 nam có ![]() cách chọn
cách chọn
Do đó có ![]() cách chọn.
cách chọn.
Chọn B.

Chọn C
Chọn mỗi tổ hai học sinh nên số phần tử của không gian mẫu là ![]()
Gọi biến cố A: “Chọn 4 học sinh từ 2 tổ sao cho 4 em được chọn có 2 nam và 2 nữ”
Khi đó, xảy ra các trường hợp sau:
TH1: Chọn 2 nam ở Tổ 1, 2 nữ ở Tổ 2. Số cách chọn là ![]()
TH2: Chọn 2 nữ ở Tổ 1, 2 nam ở Tổ 2. Số cách chọn là ![]() .
.
TH3: Chọn ở mỗi tổ 1 nam và 1 nữ. Số cách chọn là ![]()
Suy ra, n(A) = ![]()
Xác suất để xảy ra biến cố A là: ![]()