Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số phần học sinh thích cả môn Toán và môn Ngữ văn trong lớp 6A là: \(\dfrac{1}{2}.\dfrac{1}{3} = \dfrac{{1.1}}{{2.3}} = \dfrac{1}{6}\) (học sinh lớp 6A)
Vậy lớp 6A có \(\dfrac{1}{6}\) số học sinh thích cả 2 môn.

số học sinh lớp 6A thích cả môn Toán và Ngữ văn là :
\(\dfrac{1}{3}.\dfrac{1}{2}=\dfrac{1}{6}\left(hs\right)\)
\(đ/s:...\)
Chiều rộng của hình chữ nhật là:
\(\dfrac{21}{10}:\dfrac{7}{2}=\dfrac{3}{5}\left(cm\right)\)
\(đ/s:...\)

Nhận thấy 13 học sinh thích cả hai môn Toán và Văn vừa được tính trong số học sinh thích môn Toán, vừa được tính trong số học sinh thích Văn , tức là được tính 2 lần
Vậy số học sinh của lớp 6A là : 25 + 24 – 13 + 9 = 45 (học sinh)

Số học sinh của lớp 6A là:
(24 + 25 – 13) + 9 = 45 (học sinh)

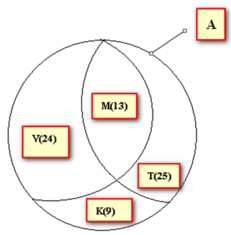
Gọi X là tập hợp tất cả các học sinh của lớp 6A;
V là tập hợp các học sinh thích môn Ngữ Văn;
T là tập hợp các học sinh thích môn Toán.
Câu hỏi ở đề bài "Lớp 6A có tất cả bao nhiêu học sinh?" đồng nghĩa với việc đi tìm số phần tử của tập hợp X.
Ta mô tả các tập hợp X, V, T như sau:
Có 15 học sinh thích Ngữ Văn nên V có 15 phần tử.
Có 20 học sinh thích Toán nên T có 20 phần tử.
Trong hình trên, phần nằm "chồng lên nhau" giữa T và V biểu thị tập hợp các học sinh vừa thích Ngữ văn vừa thích toán, tập hợp này có 8 phần tử.
Phần hình nằm trong X nhưng nằm ngoài cả T và V biểu thị tập hợp các học sinh không thích môn nào cả, tập hợp này có 10 phần tử.
Vậy số phần tử của tập hợp X là:
15 + 20 - 8 + 10 = 37.
Tức là lớp 6A có 37 học sinh.
Cre: Olm
@Ngien
Gọi X là tất cả các học sinh của lớp 6A.
V là các tập hợp các học sinh thích môn Ngữ Văn.
T là các tập hợp các học sinh thích môn Toán.
Có 15 học sinh thich môn Ngữ Văn nên V có 15 phần tử .
Có 20 học sinh thích Toán nên T có 20 phần tử.
Hình nằm trong X nhưng nằm ngoài cả T và V biểu thị tập hợp các các học sinh không thích môn nào cả , tập hợp này có 10 phần tử.
Vậy số phần tử của tập hợp X là :
15+10-8+10= 37 .
Tức là lớp 6A có 37 học sinh.