Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

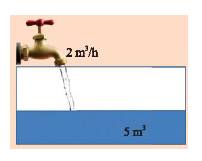
a) Lượng nước chảy vào bể sau 1 giờ là:
\(1.2 = 2\left( {{m^3}} \right)\)
b) Lượng nước chảy vào bể sau \(x\) giờ là:
\(2.x = 2x\left( {{m^3}} \right)\)
c) Lượng nước \(y\) có trong bể sau \(x\) giờ là:
\(y = 2x + 5\left( {{m^3}} \right)\).

Vì mỗi giờ vòi chảy ra=4/5 vòi chảy vào
=>Thực tế, mỗi giờ lượng nước thêm vào sẽ bằng 1/5 công suất vòi chảy vào
=>Sau 5h lượng nước chảy vào bằng công suất chảy thực của vòi chảy vào
Công suất chảy thực của vòi chảy vào là 1/8 bể/giờ
Thười gian để đầy bể khi chỉ mở vòi chảy và khóa vòi chảy ra là:
1:1/8=8(giờ)

Gọi thời gian để vòi chảy vào đầy bể nước là x (giờ) (x > 0)

Sau 5 giờ lượng nước còn lại trong bể là 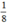 dung tích bể nên ta có phương trình:
dung tích bể nên ta có phương trình:
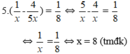
Vậy thời gian để bể đầy nước nếu chỉ mở vòi chảy là 8 giờ.
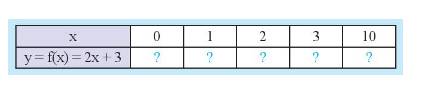

Sau khi tăng chiều dài thêm \(x\left( m \right)\) thì chiều dài mới của hình chữ nhật là \(3 + x\left( m \right)\)
Sau khi tăng chiều rộng thêm \(x\left( m \right)\) thì chiều rộng mới của hình chữ nhật là \(2 + x\left( m \right)\)
Chu vi mới của hình chữ nhật là:
\(y = \left( {3 + x + 2 + x} \right).2\)
\( \Leftrightarrow y = \left( {5 + 2x} \right).2\)
\( \Leftrightarrow y = 4x + 10\)
Vì hàm số \(y = 4x + 10\) có dạng \(y = ax + b\)với \(a,b\) là các số cho trước và \(a \ne 0\).
Nên hàm số \(y = 4x + 10\) là hàm số bậc nhất.
Do đó \(y\) là một hàm số bậc nhất theo biến số \(x\), hệ số \(a = 4;b = 10\).