Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\angle MFC=\angle MEC=90\Rightarrow MFEC\) nội tiếp
b) Ta có: \(\angle MFE=180-\angle MCE=\angle MAB\)
\(\angle FME=\angle FCE=\angle AMB\)
Xét \(\Delta AMB\) và \(\Delta MFE\):Ta có: \(\left\{{}\begin{matrix}\angle MFE=\angle MAB\\\angle FME=\angle AMB\end{matrix}\right.\)
\(\Rightarrow\Delta AMB\sim\Delta MFE\left(g-g\right)\Rightarrow\dfrac{BM}{BA}=\dfrac{ME}{FE}\Rightarrow BM.FE=ME.BA\)
c) Ta có: \(\Rightarrow\Delta AMB\sim\Delta MFE\Rightarrow\dfrac{MF}{FE}=\dfrac{MA}{AB}\Rightarrow2\dfrac{MF}{FE}=2\dfrac{MA}{AB}\)
\(\Leftrightarrow\dfrac{MF}{FQ}=\dfrac{MA}{AB}\)
Xét \(\Delta AMP\) và \(\Delta FMQ\):Ta có: \(\left\{{}\begin{matrix}\angle MFQ=\angle MAP\\\dfrac{MF}{FQ}=\dfrac{MA}{MB}\end{matrix}\right.\)
\(\Rightarrow\Delta AMP\sim\Delta FMQ\left(c-g-c\right)\)
d) Kẻ \(MD\bot AB\left(D\in AB\right)\)
Ta có: \(\angle MDA+\angle MFA=90+90=180\Rightarrow\) MDAF nội tiếp
\(\Rightarrow\angle DFA=\angle DMA=90-\angle DAM\)
Tương tự \(\Rightarrow\angle EFC=\angle EMC=90-\angle MCB\)
mà \(\angle DAM=\angle MCB\) (AMCB nội tiếp)\(\Rightarrow\angle DFA=\angle EFC\)
mà A,F,C thẳng hàng \(\Rightarrow\) \(\)D,F,E thẳng hàng
Ta có: \(\angle MQF=\angle MPA\left(\Delta MFQ\sim\Delta MAP\right)\Rightarrow\angle MQD=\angle MPD\)
\(\Rightarrow\) MDPQ nội tiếp mà \(\angle MDP=90\Rightarrow\angle PQM=90\)

1: Xét tứ giác BHEK có \(\widehat{BHE}+\widehat{BKE}=180^0\)
nên BHEK là tứ giác nội tiếp
2: Xét ΔBEA vuông tại E có EH là đường cao
nên \(BH\cdot BA=BE^2\left(1\right)\)
Xét ΔBEC vuông tại E có EK là đường cao
nên \(BK\cdot BC=BE^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BA=BK\cdot BC\)

a:góc AHM+góc AKM=180 độ
=>AHMK nội tiếp
b: góc MBH+góc ABM=180 độ
góc MCK+góc ACM=180 độ
góc ABM=góc ACM
=>góc MBH=góc MCK
mà góc MHB=góc MKC
nên ΔMHB đồng dạng vơi ΔMKC
=>MH/MK=MB/MC
=>MH*MC=MK*MB

a: góc AHM+góc AKM=180 độ
=>AHMK là tứ giác nội tiếp
b: góc HBM=180 độ-góc ABM
góc KCM=180 độ-góc ACM
góc ABM=góc ACM
=>góc HBM=góc KCM
mà góc MHB=góc MKC
nên ΔMBH đồng dạng với ΔMCK
=>MB/MC=MH/MK
=>MB*MK=MC*MH

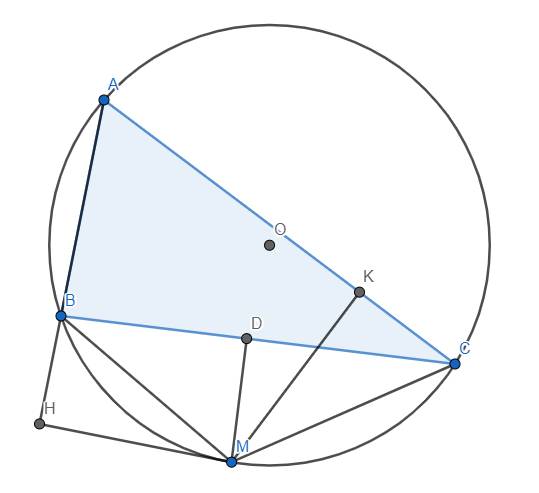
a) Theo đề bài, ta thấy \(\widehat{AHM}=\widehat{AKM}=90^o\) nên dễ dàng suy ra tứ giác AHMK nội tiếp do 2 góc đối bù nhau.
b) Do tứ giác AHMK nội tiếp nên \(\widehat{HMK}+\widehat{A}=180^o\). Tứ giác ABMC nội tiếp nên \(\widehat{BMC}+\widehat{A}=180^o\). Từ đó suy ra \(\widehat{HMK}=\widehat{BMC}\) hay \(\widehat{BMH}=\widehat{CMK}\). Lại có \(\widehat{MHB}=\widehat{MKC}=90^o\) nên \(\Delta MHB~\Delta MKC\left(g.g\right)\) \(\Rightarrow\dfrac{MH}{MK}=\dfrac{MB}{MC}\) \(\Rightarrowđpcm\)

a: góc AHM+góc AKM=180 độ
=>AHMK nội tiếp
b: Xét ΔMHB vuông tại H và ΔMKC vuông tại K có
góc HBM=góc KCM
=>ΔMHB đồng dạng vơi ΔMKC
=>MH/MK=MB/MC
=>MH*MC=MB*MK



