
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left|x\right|=2\frac{1}{3}\Rightarrow\orbr{\begin{cases}x=\frac{7}{3}\\x=-\frac{7}{3}\end{cases}}\)
\(\left|x\right|=-3\Rightarrow\orbr{\begin{cases}x=-3\\x=3\end{cases}}\)
\(\left|x-1.7\right|=2.3\Rightarrow\orbr{\begin{cases}x-1.7=2.3\\x-1.7=-2.3\end{cases}\Rightarrow\orbr{\begin{cases}x=4\\-\frac{3}{5}\end{cases}}}\)
\(\left|x+\frac{3}{4}\right|=\frac{1}{2}\Rightarrow\orbr{\begin{cases}x+\frac{3}{4}=\frac{1}{2}\\x+\frac{3}{4}=-\frac{1}{2}\end{cases}\Rightarrow\orbr{\begin{cases}x=\frac{-1}{4}\\-\frac{5}{4}\end{cases}}}\)
a) \(\left|x\right|=2\frac{1}{3}\)
\(\left|x\right|=\frac{7}{3}\)
\(\Rightarrow x=\frac{7}{3}\) hoặc \(x=-\frac{7}{3}\)
b) \(\left|x\right|=-3\)
\(\Rightarrow\) Không có giá trị x nào thỏa mãn đề bài
c) \(\left|x\right|=-3,15\)
\(\Rightarrow\) Không có giá trị x nào thỏa mãn đề bài
d) \(\left|x-1,7\right|=2,3\)
\(\Rightarrow x-1,7=2,3\) hoặc \(x-1,7=-2,3\)
Với \(x-1,7=2,3\)
\(x=2,3+1,7=4\)
Với \(x-1,7=-2,3\)
\(x=-2,3+1,7=-0,6\)
Vậy \(x\in\left\{4;-0,6\right\}\)
e) \(\left|x+\frac{3}{4}\right|-\frac{1}{2}=0\)
\(\left|x+\frac{3}{4}\right|=0+\frac{1}{2}\)
\(\left|x+\frac{3}{4}\right|=\frac{1}{2}\)
\(\Rightarrow x+\frac{3}{4}=\frac{1}{2}\) hoặc \(x+\frac{3}{4}=-\frac{1}{2}\)
Với \(x+\frac{3}{4}=\frac{1}{2}\)
\(x=\frac{1}{2}-\frac{3}{4}=\frac{2}{4}-\frac{3}{4}=\frac{-1}{4}\)
Với \(x+\frac{3}{4}=-\frac{1}{2}\)
\(x=-\frac{1}{2}-\frac{3}{4}=-\frac{2}{4}-\frac{3}{4}=-\frac{5}{4}\)
Vậy \(x\in\left\{-\frac{1}{4};-\frac{5}{4}\right\}\)

a, Vì lxl = 2\(\frac{1}{3}\)\(\Rightarrow\) \(\orbr{\begin{cases}x=\frac{7}{3}\\x=-\frac{7}{3}\end{cases}}\)\(\Rightarrow\)Vậy ...
b, Vì lxl \(\ge\) 0 mà lxl = -3 => ko tìm đc x
c, lập luận tg tự phần b
d, Vì lx-1.7l =2.3 \(\Rightarrow\)\(\orbr{\begin{cases}x-1,7=2,3\\x-1,7--2,3\end{cases}}\)\(\Rightarrow\)\(\orbr{\begin{cases}x=2,3+1,7\\x=-2,3+1,7\end{cases}}\)\(\Rightarrow\)\(\orbr{\begin{cases}x=4\\x=-0,6\end{cases}}\)Kết luận
e, Vì lx+3/4l -1/2 = 0 => lx+3/4l = 1/2 \(\Rightarrow\)\(\orbr{\begin{cases}x+\frac{3}{4}=\frac{1}{2}\\x+\frac{3}{4}=-\frac{1}{2}\end{cases}}\)\(\Rightarrow\)\(\orbr{\begin{cases}x=\frac{1}{2}-\frac{3}{4}\\x=-\frac{1}{2}-\frac{3}{4}\end{cases}}\)\(\Rightarrow\)\(\orbr{\begin{cases}x=-\frac{1}{4}\\x=-\frac{3}{4}\end{cases}}\)
Kết luận
a, x=-2 1/3 hoặc x=2 1/3
b, không tồn tại x vì /x/>=0
c, tương tự b
d,x-1,7=2,3 hoặc x-1,7=-2,3 pn tự lm tiếp ha
e,x+3/4=1/2 hoặc x+3/4=-1/2



1, \(\dfrac{a+b-c}{c}=\dfrac{a+c-b}{b}=\dfrac{b+c-a}{a}\)
=> \(\dfrac{a+b}{c}-1=\dfrac{a+c}{b}-1=\dfrac{b+c}{a}-1\)
=> \(\dfrac{a+b}{c}=\dfrac{a+c}{b}=\dfrac{b+c}{a}\)
=> \(\dfrac{a+b}{c}=\dfrac{a+c}{b}=\dfrac{b+c}{a}=\dfrac{a+b+a+c+b+c}{a+b+c}=\dfrac{2\left(a+b+c\right)}{a+b+c}=2\)
=> \(M=\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}=\dfrac{a+b}{c}\times\dfrac{a+c}{b}\times\dfrac{b+c}{a}=2.2.2=8\)
=> \(M=8\)

Bài 1:
Nếu $a+b+c=0$ thì đkđb thỏa mãn
$M=\frac{(-c)(-a)(-b)}{abc}=\frac{-(abc)}{abc}=-1$
Nếu $a+b+c\neq 0$. Áp dụng TCDTSBN:
$\frac{a+b-c}{c}=\frac{a+c-b}{b}=\frac{b+c-a}{a}=\frac{a+b-c+a+c-b+b+c-a}{c+b+a}=\frac{a+b+c}{a+b+c}=1$
$\Rightarrow a+b-c=c; a+c-b=b; b+c-a=a$
$\Leftrightarrow a+b=2c; a+c=2b; b+c=2a$
$\Rightarrow a=b=c$
$M=\frac{(a+a)(a+a)(a+a)}{aaa}=\frac{8a^3}{a^3}=8$
Bài 2a
Đặt $2x=3y=4z=t$
$\Rightarrow x=\frac{t}{2}; y=\frac{t}{3}; z=\frac{t}{4}$
Khi đó:
$|x+y+3z|=1$
$\Leftrightarrow |\frac{t}{2}+\frac{t}{3}+\frac{3t}{4}|=1$
$\Leftrightarrow |\frac{19}{12}t|=1$
$\Rightarrow t=\pm \frac{12}{19}$
Nếu $t=\frac{12}{19}$ thì:
$x=\frac{t}{2}=\frac{6}{19}; y=\frac{4}{19}; z=\frac{3}{19}$
Nếu $t=-\frac{12}{19}$ thì:
$x=\frac{t}{2}=\frac{-6}{19}; y=\frac{-4}{19}; z=\frac{-3}{19}$



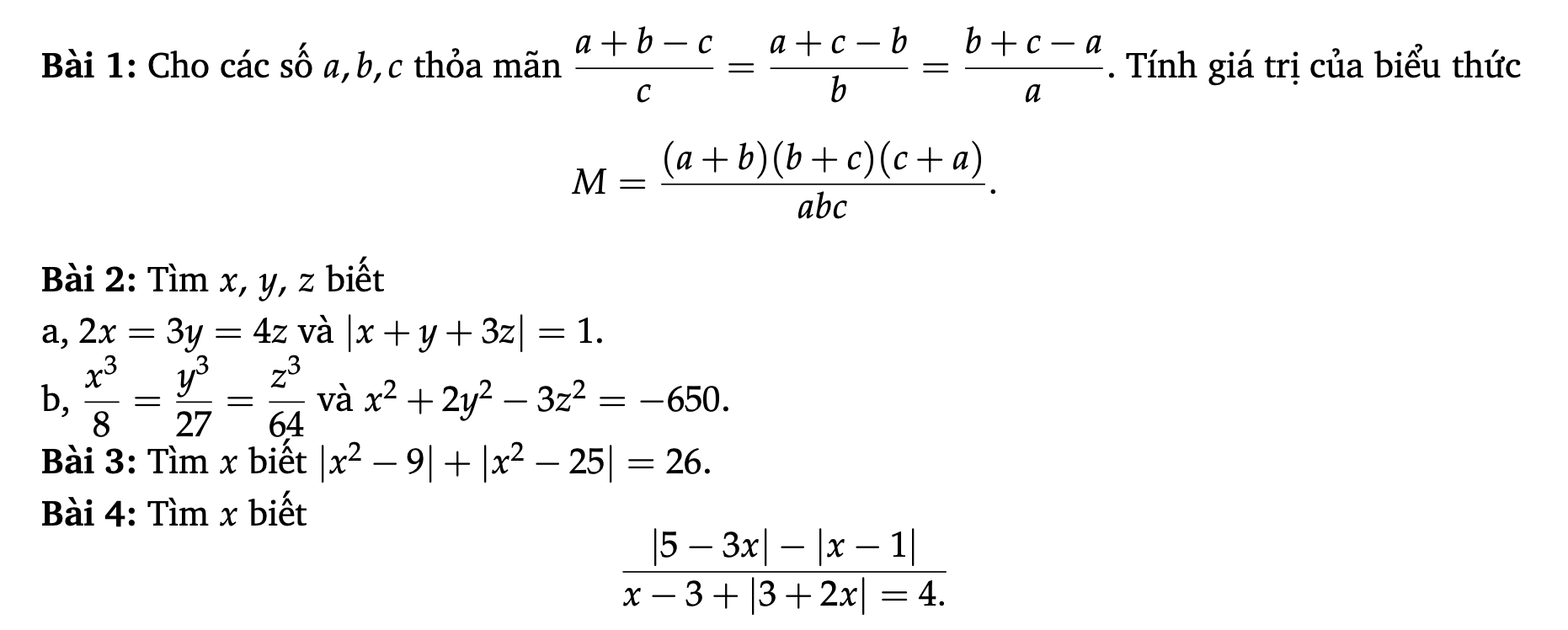
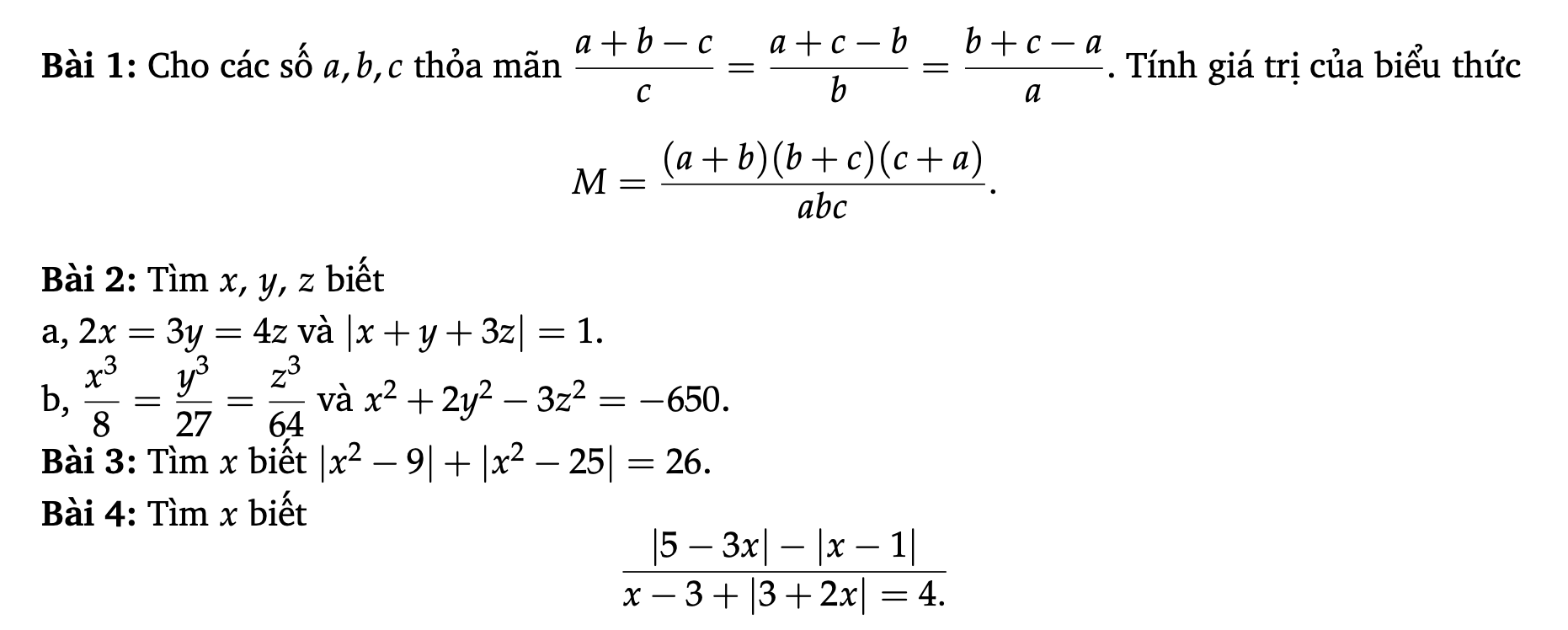
MÀ CÁI HÌNH THỨ 2 BÊN GÓC PHẢI LÀ CỦA BÀI 3 NHA