Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi E là biến cố “Người không thành thạo cả hai thứ tiếng Anh hay Pháp”.
Khi đó \(\overline E \) là biến cố “Người thành thạo tiếng Anh hoặc Pháp”.
Ta có \(\overline E = A \cup B.\)
\( \Rightarrow P\left( E \right) = 1 - P\left( {\overline E } \right) = 1 - P\left( {A \cup B} \right) = 1 - \frac{{47}}{{50}} = \frac{3}{{50}}\)
Vậy xác suất để người được chọn không thành thạo cả hai thứ tiếng Anh hay Pháp là \(\frac{3}{{50}}.\)
Đáp án B.
Sử dụng dữ kiện sau để trả lời các câu hỏi trong các Bài 8.20, 8.21.
Một lớp có 40 học sinh, trong đó có 23 học sinh thích bóng chuyền,18 học sinh thích bóng rổ, 26 học sinh thích bóng chuyền hoặc bóng rổ hoặc cả hai. Chọn ngẫu nhiên một học sinh trong lớp.

Gọi A là biến cố “Người thành thạo tiếng Anh”; B là biến cố “Người thành thạo tiếng Pháp”.
Khi đó \(P\left( A \right) = \frac{{31}}{{50}},P\left( B \right) = \frac{{21}}{{50}},P\left( {AB} \right) = \frac{5}{{50}} = \frac{1}{{10}}\)
Ta có \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = \frac{{31}}{{50}} + \frac{{21}}{{50}} - \frac{1}{{10}} = \frac{{47}}{{50}}\)
Vậy xác suất để người được chọn thành thạo ít nhất một trong hai thứ tiếng Anh hoặc Pháp là \(\frac{{47}}{{50}}.\)
Đáp án A

Đáp án D
Xác suất 2 bạn hòa nhau 1 – 0,3 – 0,4 = 0,3.
Để hai bạn dừng chơi sau 2 ván cờ thì ván 1 hòa, ván 2 không hòa
vậy xác suất là 0,3.0,7 = 0,21.

Đáp án B
Số phần tử của không gian mẫu là: ![]()
Gọi X là biến cố “cả hai bạn Việt và Nam nằm chung một bảng đấu’
Số kết quả thuận lợi cho biến cố X là: ![]()
Vậy xác suất cần tính
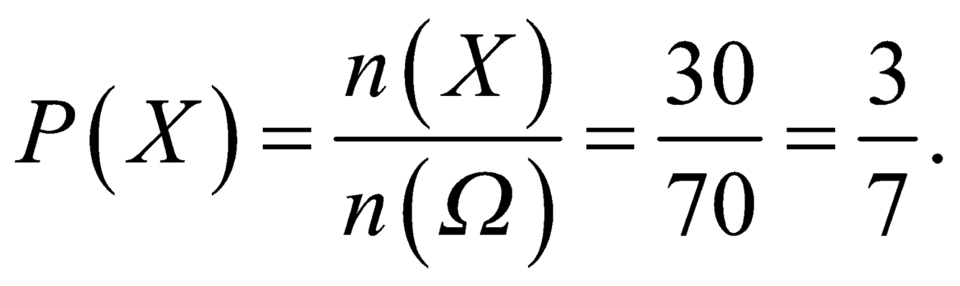
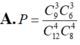
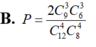
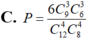
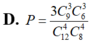

oh, cho mk lm wen nha... cho mk xem ảnh bn dc ko ạ?
mik on laptop
@NTMH