
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a,= 𝑥(5𝑥+4)
b, =4x(x2 + 6xy - 3y2 )
c,=2(𝑥3−7𝑥)
=2𝑥(𝑥2−7)
Câu 4:
a: \(5x^2+4x=x\left(5x+4\right)\)
b: \(4x^3+24x^2y-12xy^2\)
\(=4x\left(x^2+6xy-3y^2\right)\)
c: \(2x^3-14x=2x\left(x^2-7\right)\)
d: \(6x^2y-9xy^2+15x^2y^2\)
\(=3xy\left(2x-3y+5xy\right)\)


a: Xét tứ giác ANME có
\(\widehat{ANM}=\widehat{AEM}=\widehat{EAN}=90^0\)
Do đó: ANME là hình chữ nhật


<=> (x+2 ) (x2 - 3x + 5 ) - (x+2 ) x2=0
<=> (x+ 2 ) (x2-3x + 5 - x2) =0
<=> (x + 2 ) (-3x+5)=0
<=> x+2 = 0 hoặc -3x+5=0
x = -2 -3x = -5
x=5/3

Áp dụng định lý Ta-lét ta có:
\(\dfrac{AD}{DB}=\dfrac{AE}{EC}\\
\Rightarrow\dfrac{2}{4}=\dfrac{3}{x}\\
\Rightarrow x=3:\dfrac{1}{2}\\
\Rightarrow x=6\left(cm\right)\)

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>AB/HB=AC/HA
=>AB*HA=HB*AC
b: AH=căn 5^2-3^2=4cm
BI là phân giác
=>HI/HB=IA/AB
=>HI/3=IA/5=(HI+IA)/(3+5)=0,5
=>HI=1,5cm; IA=1,5cm

Câu 1:
a: 5x-2=3x+6
=>5x-3x=2+6
=>2x=8
=>\(x=\dfrac{8}{2}=4\)
b: a<=b
=>-2022a>=-2022b
=>-2022a+2021>=-2022b+2021
Câu 2:
1:
a: ĐKXĐ: x<>1
\(\dfrac{3}{x-1}+1=\dfrac{2x+5}{x-1}\)
=>\(\dfrac{3+x-1}{x-1}=\dfrac{2x+5}{x-1}\)
=>\(2x+5=x+2\)
=>x=-3(nhận)
b: |x-9|=2x-3
=>\(\left\{{}\begin{matrix}2x-3>=0\\\left(2x-3\right)^2=\left(x-9\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\\left(2x-3-x+9\right)\left(2x+3+x-9\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\\left(x+6\right)\left(3x-6\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\\left[{}\begin{matrix}x=-6\left(loại\right)\\x=2\left(nhận\right)\end{matrix}\right.\end{matrix}\right.\)
=>x=2
2:
\(\dfrac{x-3}{2}-\dfrac{3x+2}{4}< \dfrac{1}{3}\)
=>\(\dfrac{6\left(x-3\right)-3\left(3x+2\right)}{12}< \dfrac{4}{12}\)
=>6x-18-9x-6<4
=>-3x-24<4
=>-3x<28
=>\(x>-\dfrac{28}{3}\)
Câu 3:
Gọi độ dài quãng đường AB là x(km)
(Điều kiện: x>0)
Thời gian đi từ A đến B là \(\dfrac{x}{40}\left(giờ\right)\)
Thời gian ô tô đi từ B về A là \(\dfrac{x}{30}\left(giờ\right)\)
Theo đề, ta có phương trình:
\(\dfrac{x}{40}+\dfrac{x}{30}+\dfrac{1}{2}=9+\dfrac{1}{4}\)
=>\(\dfrac{7x}{120}=8,75\)
=>\(x=8,75:\dfrac{7}{120}=120\cdot1,25=150\left(nhận\right)\)
vậy: Độ dài quãng đường AB là 150km

a: \(2x^2\left(3xy+x^2-2y^2\right)\)
\(=6x^3y+2x^4-4x^2y^2\)
b: \(\dfrac{1}{3}x^2y^3\left(2x-3y+1\right)\)
\(=\dfrac{2}{3}x^3y^3-x^2y^4+\dfrac{1}{3}x^2y^3\)
h: \(\left(x-1\right)\left(x+1\right)\left(2x-3\right)\)
\(=\left(x^2-1\right)\left(2x-3\right)\)
\(=2x^3-3x^2-2x+3\)


 Mn giải giúp mik vs ạ 🥺 mình đang cần gấp. Cảm ơn mn nhiều
Mn giải giúp mik vs ạ 🥺 mình đang cần gấp. Cảm ơn mn nhiều

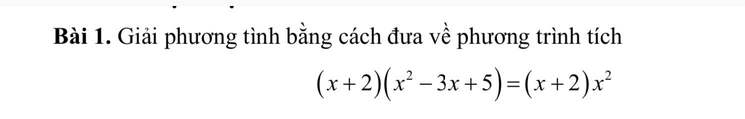

 vẽ hình giúp mik nha mik cảm ơn rất rất nhiều
vẽ hình giúp mik nha mik cảm ơn rất rất nhiều
Câu 1 :
\(a,5\left(x+2\right)=2\left(x-4\right)\)
\(\Leftrightarrow5x+10=2x-8\)
\(\Leftrightarrow5x-2x=-8-10\)
\(\Leftrightarrow3x=-18\)
\(\Leftrightarrow x=-6\)
\(b,x\left(x+2\right)+3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\end{matrix}\right.\)
Vậy \(S=\left\{3;2\right\}\)
\(c,\dfrac{2x-5}{4}-\dfrac{x+1}{3}=\dfrac{1}{2}\)
\(\Leftrightarrow3\left(2x-5\right)-4\left(x+1\right)=6\)
\(\Leftrightarrow6x-15-4x-4=6\)
\(\Leftrightarrow6x-4x=6+4+15\)
\(\Leftrightarrow2x=25\)
\(\Leftrightarrow x=\dfrac{25}{2}\)
Vậy \(S=\left\{\dfrac{25}{2}\right\}\)
\(d,\dfrac{3}{x-2}-\dfrac{6}{x+2}=\dfrac{-x}{x^2-4}\left(đkxđ:x\ne\pm2\right)\)
\(\Leftrightarrow3\left(x+2\right)-6\left(x-2\right)=-x\)
\(\Leftrightarrow3x+6-6x+12=-x\)
\(\Leftrightarrow3x-6x+x=-12-6\)
\(\Leftrightarrow-2x=-18\)
\(\Leftrightarrow x=9\left(nhận\right)\)
Vậy \(S=\left\{9\right\}\)
Câu 3 :
a, Xét ΔABD và ΔHBA có :
\(\widehat{A}=\widehat{H}=90^0\)
\(\widehat{B}:chung\)
\(\Rightarrow\Delta ABD\sim\Delta HBA\left(g-g\right)\)
b, Xét ΔADH và ΔDBC có :
\(\widehat{H}=\widehat{C}=90^0\)
\(\widehat{ADH}=\widehat{DBC}\left(AB//CD,slt\right)\)
\(\Rightarrow\Delta ADH\sim\Delta DBC\)
c, Ta có : \(\Delta ABD\sim\Delta HBA\left(cmt\right)\)
\(\Rightarrow\dfrac{AB}{BH}=\dfrac{BD}{AB}\)
\(\Rightarrow AB^2=BH.BD\)
d, Xét ΔABD vuông ở A , theo định lý Pi-ta-go ta được :
\(\Rightarrow BD=\sqrt{AB^2+AD^2}=\sqrt{12^2+9^2}=15\left(cm\right)\)
Ta có : \(\Delta ABD\sim\Delta HBA\left(cmt\right)\)
\(\Rightarrow\dfrac{AB}{BH}=\dfrac{BD}{AB}\)
hay \(\dfrac{12}{BH}=\dfrac{15}{12}\)
\(\Rightarrow BH=\dfrac{12.12}{15}=9,6\left(cm\right)\)