
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a)\(5x^2.\left(10x^4-5x^3+2\right)=50x^6-25x^5+10x^2\)
b) \(\left(x^2-5x+3\right).\left(-5x\right)=-5x^3+25x^2-15x\)
c) \(\left(5x-2y\right)\left(x^2-xy+1\right)=5x^3-5x^2y+5x-2x^2y+2xy^2-2y\\ =5x^3-7x^2y+2xy^2+5x-2y\)
d) \(\left(3x-2\right)\left(9x^2+6x-4\right)\\ =27x^3+18x^2-12x-18x^2-12x+8=27x^3+8\)
a) \(5x^2\left(10x^4-5x^3+2\right)=50x^6-25x^5+10x^2\)
b) \(\left(x^2-5x+3\right)\left(-5x\right)=-5x^3+25x^2-15x\)
c) \(\left(5x-2y\right)\left(x^2-xy+1\right)=5x^3-5x^2y+5x-2x^2y+2xy^2-2y=5x^3-7x^2y+2xy^2+5x-2y\)
d) \(\left(3x-2\right)\left(9x^2+6x-4\right)=27x^3+18x^2-12x-18x^2-12x+8=27x^3-24x+8\)

ĐKXĐ: \(x\notin\left\{0;-9\right\}\)
Ta có: \(\dfrac{1}{x+9}-\dfrac{1}{x}=\dfrac{1}{5}+\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{20x}{20x\left(x+9\right)}-\dfrac{20\left(x+9\right)}{20x\left(x+9\right)}=\dfrac{4x\left(x+9\right)+5x\left(x+9\right)}{20x\left(x+9\right)}\)
Suy ra: \(4x^2+36x+5x^2+45x=20x-20x-180\)
\(\Leftrightarrow9x^2+81x+180=0\)
\(\Leftrightarrow x^2+9x+20=0\)
\(\Leftrightarrow x^2+4x+5x+20=0\)
\(\Leftrightarrow x\left(x+4\right)+5\left(x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\left(nhận\right)\\x=-5\left(nhận\right)\end{matrix}\right.\)
Vậy: S={-4;-5}

a: Xét ΔOMN và ΔOPQ có
góc OMN=góc OPQ
góc MON=góc POQ
=>ΔOMN đồng dạng với ΔOPQ
=>OM/OP=ON/OQ=MN/PQ
=>OM*OQ=OP*ON
b: Xét ΔOMA vuông tại A và ΔOPB vuông tại B có
góc OMA=góc OPB
=>ΔOMA đồng dạng với ΔOPB
=>OM/OP=OA/OB=MN/PQ


chu vi hình vuông là
50x4=200cm
độ dài 1 cạnh hình vuông là
50:4=12,5cm
diện tích hình vuông là
12,5x12,5=156,25cm2



Bài 9:
a= 3q+1
b=3k+2
ab=(3q+1)(3k+2)
ab=9qk+6q+3k+2
=> ab chia cho 3 dư 2
Bài 10:
n(2n+3) - 2n(n+1)
= 2n2 - 3n - 2n2 - 2n
=(2n2 - 2n2) - (3n + 2n)
=-5n
Vì -5 chia hết cho 5 nên biểu thức n(2n+3) - 2n(n+1) luôn chia hết cho 5 với mọi số nguyên n
mình có thiếu sót chỗ nào thì mn giúp mình với nhé :>>






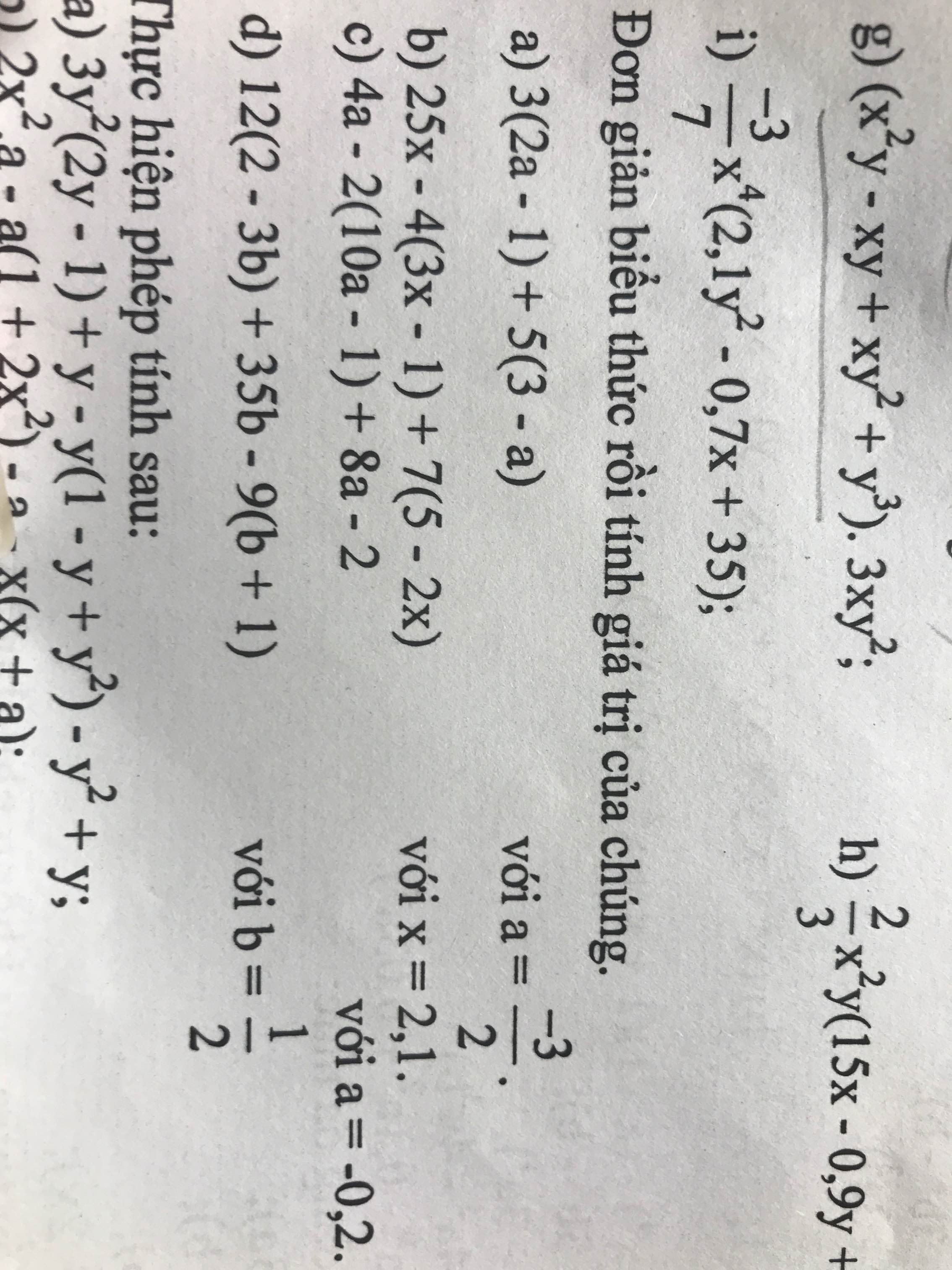


Bài 10
a; Giao của d1 với trục ox là điểm có hoành độ thỏa mãn
\(x\) - 3 = 0 ⇒ \(x\) = 3
Giao của d1 với trục oy là điểm có tung độ thỏa mãn y = 0 - 3 = -3
Giao của d2 với trục ox là điểm có hoành độ thỏa mãn
3 - \(x\) = 0 ⇒ \(x\) = 3
Giao của d2 với trục oy là điểm có tung độ thỏa mãn y = 3 - 0 = 3
Ta có đồ thị d1 và d2 như hình dưới
b; Giao của d1 và d2 là điểm có phương trình hoành độ thỏa mãn
\(x\) - 3 = 3 - \(x\)
2\(x\) = 6
\(x\) = 6 : 2
\(x\) = 3; ⇒ y = 3- 3 =0
Vậy giao của d1 và d2 là A(3;0)
Bài 9:
Giao của d1 với trục ox là điểm có hoành độ thỏa mãn
2\(x\) - 3 = 0 ⇒ \(x\) = \(\dfrac{3}{2}\)
Giao của d1 với trục oy là điểm có tung độ thỏa mãn
y = 2.0 - 3 = - 3
Giao của d2 với trục ox là điểm có hoành độ thỏa mãn
-3 - \(x\) = 0 ⇒ \(x\) = 0
Giao của d2 với trục oy là điểm có tung độ thỏa mãn
y = -3 - 0 = -3
Ta có đồ thị như hình dưới đây
Giao của d1 và d2 là điểm có hoành độ thỏa mãn phương trình
2\(x\) - 3 = -3 - \(x\)
2\(x\) + \(x\) = 0
3\(x\) =0
\(x\) = 0
⇒ y = -3 - 0
y = - 3
Vậy giao của d1 và d2 là điểm B(0; -3)