
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo đề ta có:
\(\dfrac{a}{\dfrac{1}{\dfrac{1}{2}}}=\dfrac{b}{\dfrac{1}{\dfrac{1}{5}}}=\dfrac{c}{\dfrac{1}{\dfrac{1}{7}}}\) và \(a+b-2c=70\)
Áp dụng tính chất của dãy tỉ số bằng nhay ta có:
\(\dfrac{a}{\dfrac{1}{\dfrac{1}{2}}}=\dfrac{b}{\dfrac{1}{\dfrac{1}{5}}}=\dfrac{c}{\dfrac{1}{\dfrac{1}{7}}}=\dfrac{a}{2}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{2c}{2.7}=\dfrac{a+b-2c}{2+5-14}=\dfrac{70}{-7}=-10\)
\(\dfrac{a}{2}=-10\Rightarrow a=\left(-10\right).2=-20\)
\(\dfrac{b}{5}=-10\Rightarrow b=\left(-10\right).5=-50\)
\(\dfrac{c}{7}=-10\Rightarrow c=\left(-10\right).7=-70\)
Vậy \(a=-20;b=-50;c=-70\)

Bài 1 :
a,Có \(AD\) chung , mà \(AB=AC;DB=DC\)
\(\Rightarrow\Delta ABC=\Delta ADC\)
Do đó \(\widehat{ABD}=\widehat{ACD}\)
b,\(AD\) là cạnh chung của 2\(\Delta:\Delta ABD,\Delta ACD\)
\(\Rightarrow AD\) là phân giác của \(\widehat{BAC}\)
Bài 2:
Ta có : \(EF=HG,\widehat{EFO}=\widehat{GHO}\)
Theo TH thứ 2 của 2 tam giác bằng nhau ta có : cạnh - góc - cạnh
\(\Rightarrow OE=OG\)
Bài 3: Có hình ko bn ,mk dựa vào hình lm ko mk lười vẽ hình lắm =(((((((


\(\widehat{B_2}=\widehat{B_4}=60^0\left(đối.đỉnh\right)\\ \widehat{B_2}+\widehat{B_1}=180^0\left(kề.bù\right)\\ \Rightarrow\widehat{B_1}=180^0-60^0=120^0\\ \Rightarrow\widehat{B_3}=\widehat{B_1}=120^0\left(đối.đỉnh\right)\)
Vì a//b nên \(\widehat{B_2}=\widehat{A_4}=60^0;\widehat{B_1}=\widehat{A_3}=120^0\left(so.le.trong\right)\)
Ta có \(\left\{{}\begin{matrix}\widehat{A_2}=\widehat{A_4}=60^0\\\widehat{A_1}=\widehat{A_3}=120^0\end{matrix}\right.\left(đối.đỉnh\right)\)

Bài 1:
Mình có hình cho câu a) thôi nha.
a) Xét 2 \(\Delta\) \(ABD\) và \(ACD\) có:
\(AB=AC\left(gt\right)\)
\(BD=CD\) (vì D là trung điểm của \(BC\))
Cạnh AD chung
=> \(\Delta ABD=\Delta ACD\left(c-c-c\right)\)
=> \(\widehat{BAD}=\widehat{CAD}\) (2 góc tương ứng).
=> \(AD\) là tia phân giác của \(\widehat{BAC}.\)
b) Vì \(\widehat{BAD}=\widehat{CAD}\left(cmt\right)\)
=> \(\widehat{MAD}=\widehat{NAD}.\)
Xét 2 \(\Delta\) \(AMD\) và \(AND\) có:
\(AM=AN\left(gt\right)\)
\(\widehat{MAD}=\widehat{NAD}\left(cmt\right)\)
Cạnh AD chung
=> \(\Delta AMD=\Delta AND\left(c-g-c\right)\)
=> \(\widehat{AMD}=\widehat{AND}\) (2 góc tương ứng).
Mà \(\widehat{AMD}=90^0\left(gt\right)\)
=> \(\widehat{AND}=90^0.\)
=> \(DN\perp AN\)
Hay \(DN\perp AC.\)
Chúc bạn học tốt!



 2
2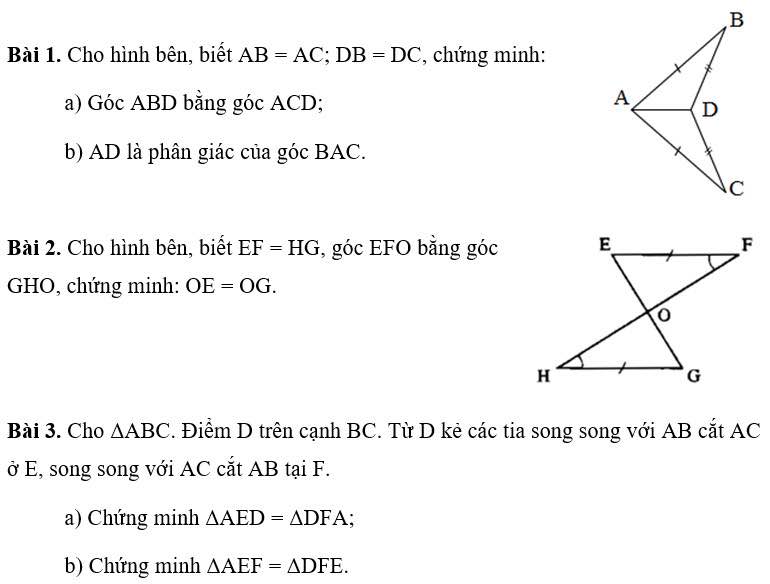 Các bạn làm giúp mình mấy bài này gấp nhé chiều nay mình phải nộp rồi
Các bạn làm giúp mình mấy bài này gấp nhé chiều nay mình phải nộp rồi




 giúp mik với mai mik phải nộp rồi😇😂😦😢
giúp mik với mai mik phải nộp rồi😇😂😦😢