
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,B=4\sqrt{x+1}-3\sqrt{x+1}+\sqrt{x+1}+2\sqrt{x+1}=4\sqrt{x+1}\\ b,B=8\Leftrightarrow4\sqrt{x+1}=8\\ \Leftrightarrow\sqrt{x+1}=2\\ \Leftrightarrow x+1=4\\ \Leftrightarrow x=3\left(tm\right)\)

\(M=\left(\dfrac{a-1}{2\sqrt{a}}\right)^2\cdot\dfrac{a-2\sqrt{a}+1-a-2\sqrt{a}-1}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\\ M=\dfrac{\left(a-1\right)^2}{4a}\cdot\dfrac{-4\sqrt{a}}{a-1}=\dfrac{1-a}{\sqrt{a}}\)
anh có thể ghi thêm các bước trước khi ra đc mấy cái này ko ạ tại rút gọn quá e ch hỉu ạ e c.ơn

\(K=\dfrac{2\sqrt{3a+1}+2\sqrt{3b+1}+2\sqrt{3c+1}}{2}\)\(\le\)\(\dfrac{3a+1+4+3b+1+4+3c+1+4}{4}=\dfrac{24}{4}=6\)
Vậy \(K_{max}=6\)
Dấu bằng xảy ra khi a=b=c=1

1, Với x > 0 ; x khác 4
\(A=\left(\dfrac{\sqrt{x}-1}{x-4}-\dfrac{\sqrt{x}+1}{\left(\sqrt{x}+2\right)^2}\right):\dfrac{x\sqrt{x}}{\left(x-4\right)^2}\)
\(=\left(\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)-\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(x-4\right)\left(\sqrt{x}+2\right)}\right):\dfrac{x\sqrt{x}}{\left(x-4\right)^2}\)
\(=\dfrac{x+\sqrt{x}-2-x+\sqrt{x}+2}{\left(x-4\right)\left(\sqrt{x}+2\right)}:\dfrac{x\sqrt{x}}{\left(x-4\right)^2}\)
\(=\dfrac{2\sqrt{x}\left(x-4\right)^2}{x\sqrt{x}\left(x-4\right)\left(\sqrt{x}+2\right)}=\dfrac{2\left(\sqrt{x}-2\right)}{x}\)
2, Ta có \(x=4+2\sqrt{3}\Rightarrow\sqrt{x}=\sqrt{4+2\sqrt{3}}=\sqrt{3}+1\)
Thay vào ta được \(A=\dfrac{2\left(\sqrt{3}-1\right)}{4+2\sqrt{3}}=-5+3\sqrt{3}\)
3, Ta có \(\dfrac{2\left(\sqrt{x}-2\right)}{x}-\dfrac{1}{4}\ge0\Leftrightarrow\dfrac{8\left(\sqrt{x}-2\right)-x}{4x}\ge0\)
\(\Rightarrow-x+8\sqrt{x}-16\ge0\Leftrightarrow-\left(\sqrt{x}-4\right)^2\ge0\)
\(\Leftrightarrow\left(\sqrt{x}-4\right)^2\le0\Leftrightarrow\sqrt{x}-4\le0\Leftrightarrow x\le16\)
Kết hợp đk vậy 0 < x =< 16 ; x khác 4

Ta có: ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=30^0\)
Xét ΔABC vuông tại A có
\(AB=BC\cdot\sin30^0\)
\(\Leftrightarrow BC=4:\dfrac{1}{2}=8\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=8^2-4^2=48\)
hay \(AC=4\sqrt{3}\left(cm\right)\)

1: Thay x=4 vào A, ta được:
\(A=\dfrac{6}{4+3\cdot2}=\dfrac{6}{10}=\dfrac{3}{5}\)
2: \(B=\dfrac{2\sqrt{x}-2\sqrt{x}+6}{x-9}=\dfrac{6}{x-9}\)

1: góc AEB=1/2*180=90 độ
góc MOA+góc MEA=180 độ
=>OAEM nội tiếp
2: Xét ΔOAE và ΔOFB có
góc OAE=góc OFB
góc O chung
=>ΔOAE đồng dạng với ΔOFB
=>OA/OF=OE/OB
=>OE*OF=OA*OB=2R*4R=8R^2
Xét ΔBAE và ΔBMO có
góc BAE=góc BMO
góc ABE chung
=>ΔBAE đồng dạng với ΔBMO
=>BA/BM=BE/BO
=>BM*BE=BA*BO=8R^2
=>OE*OF+BE*BM=16R^2



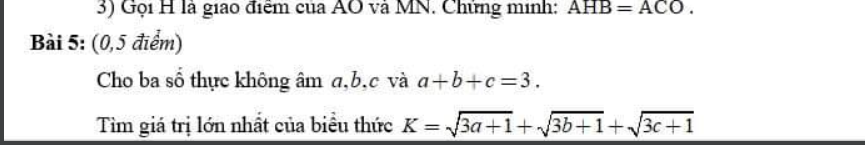
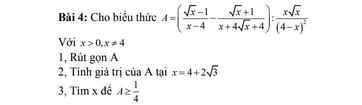 Mn giúp e với
Mn giúp e với 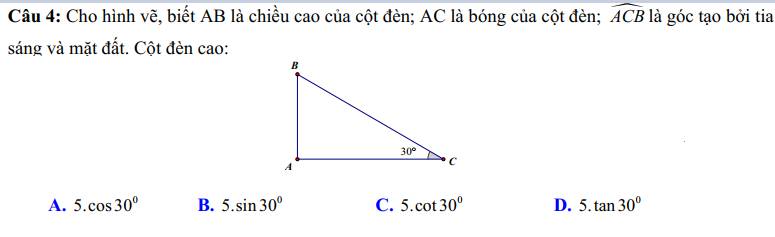


Bài 1:
a) Ta có: \(\left\{{}\begin{matrix}3x+2y=1\\x-y=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x+2y=1\\3x-3y=-\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5y=\dfrac{5}{2}\\x-y=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{5}{2}:5=\dfrac{5}{2}\cdot\dfrac{1}{5}=\dfrac{1}{2}\\x=-\dfrac{1}{2}+y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}+\dfrac{1}{2}=0\\y=\dfrac{1}{2}\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{2}\end{matrix}\right.\)
b) Ta có: \(\left\{{}\begin{matrix}3x-4y=11\\4x-3y=17\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}12x-16y=44\\12x-9y=51\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-7y=-7\\3x-4y=11\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=1\\3x=11+4\cdot y=11+4\cdot1=15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=1\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=5\\y=1\end{matrix}\right.\)