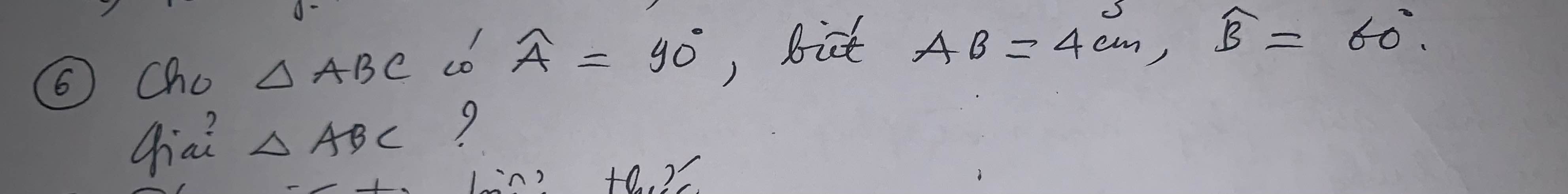Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c: \(\Leftrightarrow\left\{{}\begin{matrix}8x-2\left|y+2\right|=6\\x+2\left|y+2\right|=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x=9\\x+2\left|y+2\right|=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y+2\in\left\{1;-1\right\}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y\in\left\{-1;-3\right\}\end{matrix}\right.\)
a: \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x-3}=2\\\dfrac{1}{2\left|y\right|-3}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-3=2\\2\left|y\right|=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y\in\left\{2;-2\right\}\end{matrix}\right.\)

\(K=\dfrac{2\sqrt{3a+1}+2\sqrt{3b+1}+2\sqrt{3c+1}}{2}\)\(\le\)\(\dfrac{3a+1+4+3b+1+4+3c+1+4}{4}=\dfrac{24}{4}=6\)
Vậy \(K_{max}=6\)
Dấu bằng xảy ra khi a=b=c=1

1, Với x > 0 ; x khác 4
\(A=\left(\dfrac{\sqrt{x}-1}{x-4}-\dfrac{\sqrt{x}+1}{\left(\sqrt{x}+2\right)^2}\right):\dfrac{x\sqrt{x}}{\left(x-4\right)^2}\)
\(=\left(\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)-\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(x-4\right)\left(\sqrt{x}+2\right)}\right):\dfrac{x\sqrt{x}}{\left(x-4\right)^2}\)
\(=\dfrac{x+\sqrt{x}-2-x+\sqrt{x}+2}{\left(x-4\right)\left(\sqrt{x}+2\right)}:\dfrac{x\sqrt{x}}{\left(x-4\right)^2}\)
\(=\dfrac{2\sqrt{x}\left(x-4\right)^2}{x\sqrt{x}\left(x-4\right)\left(\sqrt{x}+2\right)}=\dfrac{2\left(\sqrt{x}-2\right)}{x}\)
2, Ta có \(x=4+2\sqrt{3}\Rightarrow\sqrt{x}=\sqrt{4+2\sqrt{3}}=\sqrt{3}+1\)
Thay vào ta được \(A=\dfrac{2\left(\sqrt{3}-1\right)}{4+2\sqrt{3}}=-5+3\sqrt{3}\)
3, Ta có \(\dfrac{2\left(\sqrt{x}-2\right)}{x}-\dfrac{1}{4}\ge0\Leftrightarrow\dfrac{8\left(\sqrt{x}-2\right)-x}{4x}\ge0\)
\(\Rightarrow-x+8\sqrt{x}-16\ge0\Leftrightarrow-\left(\sqrt{x}-4\right)^2\ge0\)
\(\Leftrightarrow\left(\sqrt{x}-4\right)^2\le0\Leftrightarrow\sqrt{x}-4\le0\Leftrightarrow x\le16\)
Kết hợp đk vậy 0 < x =< 16 ; x khác 4


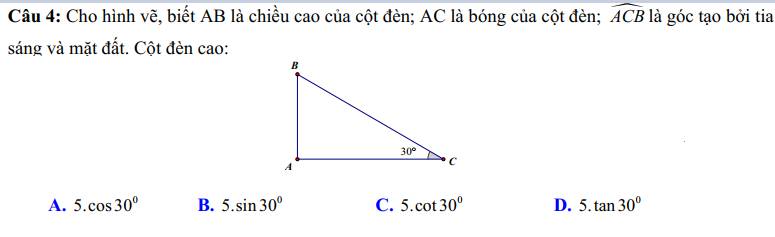
Ta có: ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=30^0\)
Xét ΔABC vuông tại A có
\(AB=BC\cdot\sin30^0\)
\(\Leftrightarrow BC=4:\dfrac{1}{2}=8\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=8^2-4^2=48\)
hay \(AC=4\sqrt{3}\left(cm\right)\)
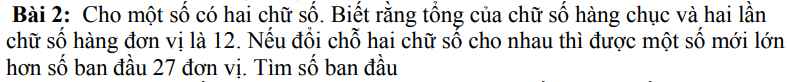 Mn giúp e với ạ
Mn giúp e với ạ
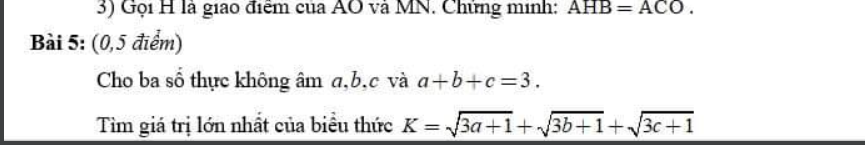
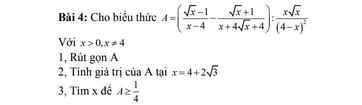 Mn giúp e với
Mn giúp e với