
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phương trình bậc hai có dạng: a\(x^2\) + b\(x\) + c
Bước 1: Đưa nó về bình phương của một tổng hoặc một hiệu cộng với một số nào đó. nếu a > 0 thì em sẽ tìm giá trị nhỏ nhất; nếu a < 0 thì em sẽ tìm giá trị lớn nhất
Bước 2: lập luận chỉ ra giá trị lớn nhất hoặc nhỏ nhất
Bước 3: kết luận
Giải:
A = 3\(x^2\) - 5\(x\) + 3 Vì a = 3 > 0 vậy biểu thức A chỉ tồn tại giá trị nhỏ nhất
A = 3\(x^2\) - 5\(x\) + 3
A = 3.(\(x\)2 - 2.\(x\).\(\dfrac{5}{6}\) + \(\dfrac{25}{36}\)) + \(\dfrac{11}{12}\)
A = 3.(\(x\) - \(\dfrac{5}{6}\))2 + \(\dfrac{11}{12}\)
Vì (\(x-\dfrac{5}{6}\))2 ≥ 0 ⇒ 3.(\(x\) - \(\dfrac{5}{6}\))2 ≥ 0 ⇒ 3.(\(x-\dfrac{5}{6}\))2 + \(\dfrac{11}{12}\) ≥ \(\dfrac{11}{12}\)
Amin = \(\dfrac{11}{12}\) ⇔ \(x\) = \(\dfrac{5}{6}\)

Câu c mình làm rồi: Mn ơi, hướng dẫn em cách để giống mẫu đi ạ! - Hoc24
\(d,\dfrac{x}{x^3-27}=\dfrac{x}{\left(x-3\right)\left(x^2+3x+9\right)}=\dfrac{x\left(x-3\right)}{\left(x-3\right)^2\left(x^2+3x+9\right)}\\ \dfrac{x+2}{x^2-6x+9}=\dfrac{x+2}{\left(x-3\right)^2}=\dfrac{\left(x+2\right)\left(x^2+3x+9\right)}{\left(x-3\right)^2\left(x^2+3x+9\right)}\\ \dfrac{x-1}{x^2+3x+9}=\dfrac{\left(x-1\right)\left(x-3\right)^2}{\left(x-3\right)^2\left(x^2+3x+9\right)}\)
\(f,\dfrac{x+2}{x^2-3x+2}=\dfrac{x+2}{\left(x-1\right)\left(x-2\right)}=\dfrac{\left(x+2\right)\left(2x-3\right)}{\left(x-1\right)\left(x-2\right)\left(2x-3\right)}\\ \dfrac{x}{-2x^2+5x-3}=\dfrac{-x}{\left(2x-3\right)\left(x-1\right)}=\dfrac{-x\left(x-2\right)}{\left(2x-3\right)\left(x-1\right)\left(x-2\right)}\\ \dfrac{2x+1}{-2x^2+7x-6}=\dfrac{-\left(2x+1\right)}{\left(x-2\right)\left(2x-3\right)}=\dfrac{-\left(2x+1\right)\left(x-1\right)}{\left(x-1\right)\left(x-2\right)\left(2x-3\right)}\)
\(\dfrac{a+x}{6x^2-ax-2a^2}=\dfrac{\left(a+x\right)}{\left(2x+a\right)\left(3x-2a\right)}\)
\(\dfrac{a-x}{3x^2+4ax-4a^2}=\dfrac{a-x}{\left(x+2a\right)\left(3x-2a\right)}\)
Do đó ta quy đồng:
\(\dfrac{a+x}{6x^2-ax-2a^2}=\dfrac{\left(a+x\right)\left(x+2a\right)}{\left(x+2a\right)\left(2x+a\right)\left(3x-2a\right)}\)
\(\dfrac{a-x}{3x^2+4ax-4a^2}=\dfrac{\left(a-x\right)\left(2x+a\right)}{\left(x+2a\right)\left(2x+a\right)\left(3x-2a\right)}\)

Theo bài ra ta có : a = 5k + 4
Khi đó : a2 = ( 5k + 4 )2
=> a2 = 25 k2 + 40k + 16
=> a2 = 5 . ( 5k2 + 8k + 3 ) + 1
Suy ra a2 chia cho 5 dư 1 ( ĐPCM )

\(\dfrac{x+1}{2x^2-x^4}=\dfrac{x+1}{x^2\left(2-x^2\right)}=\dfrac{-\left(x+1\right)\left(x^4+2x^2+4\right)}{x^2\left(x^2-2\right)\left(x^4+2x^2+4\right)}\\ \dfrac{x}{x^4+2x^2+4}=\dfrac{x^3\left(x^2-2\right)}{x^2\left(x^2-2\right)\left(x^4+2x^2+4\right)}\\ \dfrac{2x-1}{x^7-8x}=\dfrac{2x-1}{x\left(x^6-8\right)}=\dfrac{x\left(2x-1\right)}{x^2\left(x^2-2\right)\left(x^4+2x^2+4\right)}\)

a: Xét ΔBAC có
D là trung điểm của AB
M là trung điểm của AC
Do đó: DM là đường trung bình của ΔABC
Suy ra: DM//BC và \(DM=\dfrac{BC}{2}=3.5\left(cm\right)\)

a) \(\left\{{}\begin{matrix}\dfrac{x}{2}=\dfrac{y}{3}\Rightarrow\dfrac{x}{10}=\dfrac{y}{15}\\\dfrac{y}{5}=\dfrac{z}{7}\Rightarrow\dfrac{y}{15}=\dfrac{z}{21}\end{matrix}\right.\Rightarrow\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}=\dfrac{x+y+z}{10+15+21}=\dfrac{92}{46}=2\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{10}=2\Rightarrow x=2.10=20\\\dfrac{y}{15}=2\Rightarrow y=2.15=30\\\dfrac{z}{21}=2\Rightarrow z=2.21=42\end{matrix}\right.\)
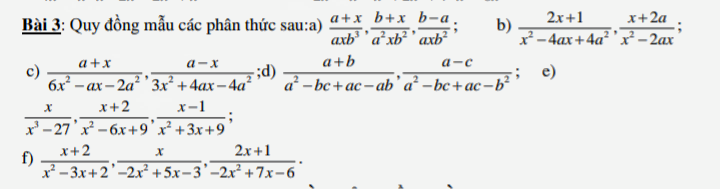






\(a,\dfrac{a+x}{axb^3}=\dfrac{a\left(a+x\right)}{a^2xb^3};\dfrac{b+x}{a^2xb^2}=\dfrac{b\left(b+x\right)}{a^2xb^3};\dfrac{b-a}{axb^2}=\dfrac{ab\left(b-a\right)}{a^2xb^3}\\ b,\dfrac{2x+1}{x^2-4ax+4a^2}=\dfrac{x\left(2x+1\right)}{x\left(x-2a\right)^2};\dfrac{x+2a}{x^2-2ax}=\dfrac{\left(x+2a\right)\left(x-2a\right)}{x\left(x-2a\right)^2}\\ c,\dfrac{a+x}{6x^2-ax-2a^2}=\dfrac{a+x}{\left(3x-2a\right)\left(2x+a\right)}=\dfrac{\left(a+x\right)\left(x+2a\right)}{\left(3x-2a\right)\left(2x+a\right)}\\ \dfrac{a-x}{3x^2+4ax-4a^2}=\dfrac{a-x}{\left(3x-2a\right)\left(x+2a\right)}=\dfrac{\left(a-x\right)\left(2x+a\right)}{\left(3x-2a\right)\left(x+2a\right)\left(2x+a\right)}\)