
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABE và ΔADC có
AB/AD=AE/AC
góc A chung
Do đó:ΔABE\(\sim\)ΔADC
b: Ta có: ΔABE\(\sim\)ΔADC
nên AB/AD=BE/DC
hay \(AB\cdot DC=AD\cdot BE\)

a) Xét 2 tam giác CKB và tam giác BAD có
Góc DAB = góc BKC = 90o
Góc ABD = góc CBD (BD là đường chéo hình chữ nhật ABCD => Tính chất)
=> Tam giác CKB đồng dạng với tam giác BAD

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: BC=căn 15^2+20^2=25cm
BH=AB^2/BC=15^2/25=9cm
c: Xét ΔBKH vuông tại K và ΔBAC vuông tại A có
góc B chung
=>ΔBKH đồng dạng với ΔBAC
=>S BKH/S BAC=(BH/BC)^2=(9/25)^2=81/625
=>S AKHC/S BAC=1-81/625=544/625
S ABC=1/2*AB*AC=1/2*15*20=150cm2
=>S AKHC=544/625*150=130,56cm2

a: Xét ΔADB và ΔBCD có
góc DAB=góc CBD
góc ABD=góc BDC
=>ΔADB đồng dạng với ΔBCD
b: ΔADB đồng dạng với ΔBCD
=>AD/BC=DB/CD=AB/BD
=>3,5/BC=5/DC=2,5/5=1/2
=>BC=7cm; DC=10cm

\(\dfrac{AM}{AC}=\dfrac{AM}{AK}.\dfrac{AK}{AC}=\dfrac{AI}{AB}.\dfrac{AK}{AC}\)
\(\dfrac{AN}{AB}=\dfrac{AN}{AI}.\dfrac{AI}{AB}=\dfrac{AK}{AC}.\dfrac{AI}{IB}\)
\(\Rightarrow\dfrac{AM}{AC}=\dfrac{AN}{AB}\Rightarrow\)MN//AB.



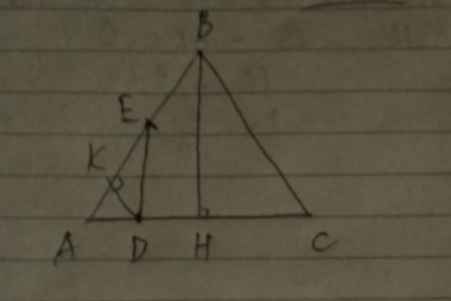



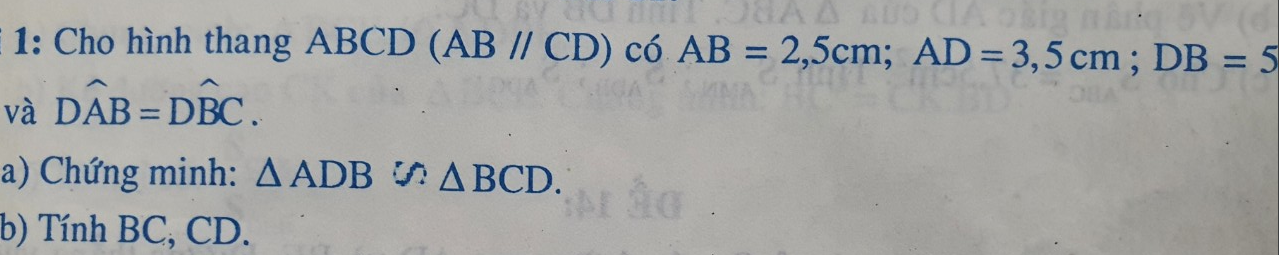
 vẽ hình nữa với ạ
vẽ hình nữa với ạ
a: Xét ΔAHM vuông tại M và ΔABH vuông tại H có
\(\widehat{HAM}\) chung
Do đó: ΔAHM đồng dạng với ΔABH
Xét ΔANH vuông tại N và ΔAHC vuông tại H có
\(\widehat{NAH}\) chung
Do đó: ΔANH đồng dạng với ΔABC
b: Ta có: ΔAHM đồng dạng với ΔABH
=>\(\dfrac{AH}{AB}=\dfrac{AM}{AH}\)
=>\(AH^2=AM\cdot AB\left(1\right)\)
Ta có: ΔANH đồng dạng với ΔAHC
=>\(\dfrac{AN}{AH}=\dfrac{AH}{AC}\)
=>\(AH^2=AN\cdot AC\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
c: \(AM\cdot AB=AN\cdot AC\)
=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN và ΔACB có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
\(\widehat{MAN}\) chung
Do đó: ΔAMN đồng dạng với ΔACB