
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4.2:
a: x^2-x+1=x^2-x+1/4+3/4
=(x-1/2)^2+3/4>=3/4>0 với mọi x
=>x^2-x+1 ko có nghiệm
b: 3x-x^2-4
=-(x^2-3x+4)
=-(x^2-3x+9/4+7/4)
=-(x-3/2)^2-7/4<=-7/4<0 với mọi x
=>3x-x^2-4 ko có nghiệm
5:
a: x^2+y^2=25
x^2-y^2=7
=>x^2=(25+7)/2=16 và y^2=16-7=9
x^4+y^4=(x^2)^2+(y^2)^2
=16^2+9^2
=256+81
=337
b: x^2+y^2=(x+y)^2-2xy
=1^2-2*(-6)
=1+12=13
x^3+y^3=(x+y)^3-3xy(x+y)
=1^3-3*1*(-6)
=1+18=19

\(1,\) Ta có \(2022\equiv1\left(mod47\right)\)
\(\Rightarrow2022^{2021}\equiv1\left(mod47\right)\)
Vậy \(2022^{2021}:47\) dư 1
\(2,\) Thay \(x=1\) vào nhị thức, ta được \(\left(5x-6\right)^{2021}=\left(-1\right)^{2021}=-1\)
Vậy tổng các hệ số là \(-1\)
\(1,\left(a+b-2c\right)^3+\left(b+c-2a\right)^3+\left(c+a-2b\right)^3\)
Đặt \(a+b-2c=x;b+c-2a=y;c+a-2b=z\Leftrightarrow z=x+y\), pt trở thành:
\(x^3+y^3+z^3\\ =\left(x+y\right)^3-3xy\left(x+y\right)+z^3\\ =-z^3-3xy\left(-z\right)+z^3\\ =3xyz\\ =3\left(a+b-2c\right)\left(b+c-2a\right)\left(a+c-2b\right)\)
\(2,\left(a+b+c\right)^3+\left(a-b-c\right)^3+\left(b-c-a\right)^3+\left(c-a-b\right)^3\\ =8a^3-3\left(a+b+c\right)\left(a-b-c\right)\cdot2a-8a^3-3\left(b-c-a\right)\left(c-a-b\right)\left(-2a\right)\\ =-6a\left\{a^2-\left(b+c\right)^2-\left[\left(-a\right)^2-\left(b-c\right)^2\right]\right\}\\ =-6a\left[a^2-a^2+\left(b-c\right)^2-\left(b+c\right)^2\right]\\ =-6a\left(b-c+b+c\right)\left[b-c-\left(b+c\right)\right]=24abc\)

a)\(5x^2.\left(10x^4-5x^3+2\right)=50x^6-25x^5+10x^2\)
b) \(\left(x^2-5x+3\right).\left(-5x\right)=-5x^3+25x^2-15x\)
c) \(\left(5x-2y\right)\left(x^2-xy+1\right)=5x^3-5x^2y+5x-2x^2y+2xy^2-2y\\ =5x^3-7x^2y+2xy^2+5x-2y\)
d) \(\left(3x-2\right)\left(9x^2+6x-4\right)\\ =27x^3+18x^2-12x-18x^2-12x+8=27x^3+8\)
a) \(5x^2\left(10x^4-5x^3+2\right)=50x^6-25x^5+10x^2\)
b) \(\left(x^2-5x+3\right)\left(-5x\right)=-5x^3+25x^2-15x\)
c) \(\left(5x-2y\right)\left(x^2-xy+1\right)=5x^3-5x^2y+5x-2x^2y+2xy^2-2y=5x^3-7x^2y+2xy^2+5x-2y\)
d) \(\left(3x-2\right)\left(9x^2+6x-4\right)=27x^3+18x^2-12x-18x^2-12x+8=27x^3-24x+8\)

3:
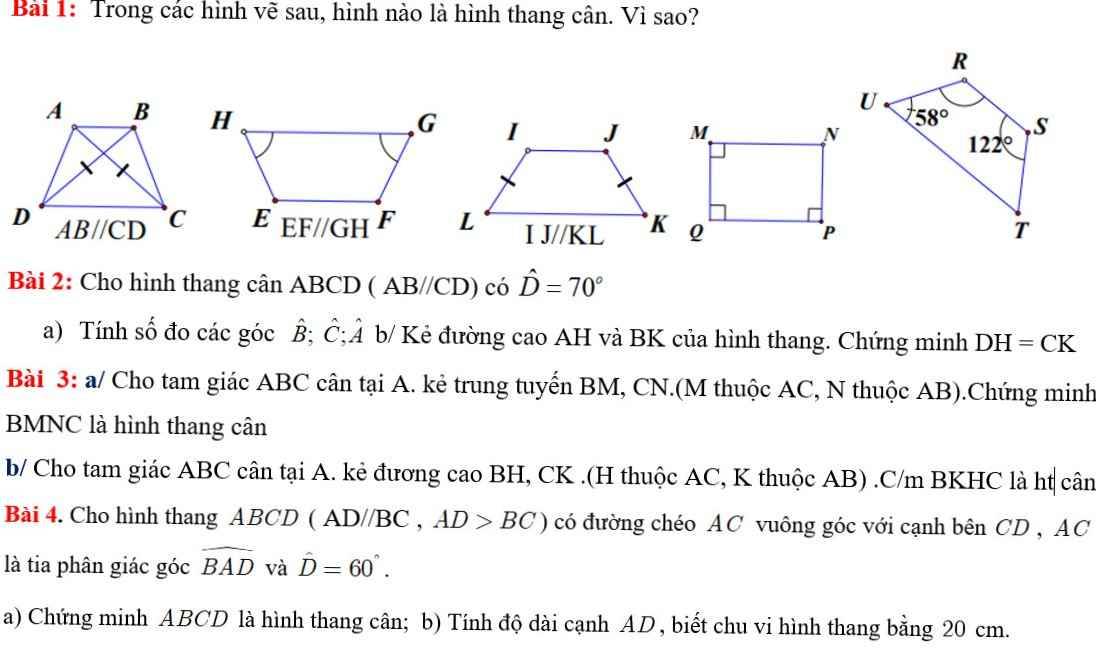
a: Xét ΔABC có M,N lần lượt là trung điểm của AC,AB
nên MN là đường trung bình
=>MN//BC và MN=BC/2
Xét tứ giác BNMC có
NM//BC
góc NBC=góc MCB
=>BNMC là hình thang cân
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
=>ΔAHB=ΔAKC
=>AH=AK
Xét ΔABC có AH/AC=AK/AB
nên KH//BC
Xét tứ giác BKHC có
HK//BC
HB=KC
=>BKHC là hình thang cân
2:
a: ABCD là hình thang cân
=>góc D=góc C=70 độ
góc A=góc B=180-70=110 độ
b: Xét ΔAHD vuông tại H và ΔBKC vuông tại K có
AD=BC
góc D=góc C
=>ΔAHD=ΔBKC
=>DH=CK

1.
\(2n+1\) luôn lẻ \(\Rightarrow2n+1=\left(2a+1\right)^2=4a^2+4a+1\Rightarrow n=2a\left(a+1\right)\)
\(\Rightarrow n\) chẵn \(\Rightarrow n+1\) lẻ \(\Rightarrow\) là số chính phương lẻ
\(\Rightarrow n+1=\left(2b+1\right)^2=4b^2+4b+1\)
\(\Rightarrow n=4b\left(b+1\right)\)
Mà \(b\left(b+1\right)\) là tích 2 số tự nhiên liên tiếp \(\Rightarrow\) luôn chẵn
\(\Rightarrow4b\left(b+1\right)⋮8\Rightarrow n⋮8\)
Mặt khác số chính phương chia 3 chỉ có các số dư 0 và 1
Mà \(\left(n+1\right)+\left(2n+1\right)=3n+2\) chia 3 dư 2
\(\Rightarrow n+1\) và \(2n+1\) đều chia 3 dư 1
\(\Rightarrow n⋮3\)
\(\Rightarrow n⋮24\) do 3 và 8 nguyên tố cùng nhau

Câu 20:
Ta có: \(\widehat{A}-\widehat{B}=40^0\Rightarrow\widehat{B}=\widehat{A}-40^0\)
\(\widehat{A}=2\widehat{C}\Rightarrow\widehat{C}=\frac{\widehat{A}}{2}\)
Vì AB//CD (gt) \(\Rightarrow\widehat{A}+\widehat{D}=180^0\)(hai góc trong cùng phía)\(\Rightarrow\widehat{D}=180^0-\widehat{A}\)
Tứ giác ABCD \(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\Rightarrow\widehat{A}+\left(\widehat{A}-40^0\right)+\frac{\widehat{A}}{2}+\left(180^0-\widehat{A}\right)=360^0\)
Và đến đây bạn dễ dàng tìm được góc A và từ đó suy ra được góc D.
Câu 29: Ta có:
\(\hept{\begin{cases}xy+x+y=3\\yz+y+z=8\\xz+x+z=15\end{cases}}\Leftrightarrow\hept{\begin{cases}xy+x+y+1=4\\yz+y+z+1=9\\xz+x+z+1=16\end{cases}\Leftrightarrow}\hept{\begin{cases}x\left(y+1\right)+\left(y+1\right)=4\\y\left(z+1\right)+\left(z+1\right)=9\\x\left(z+1\right)+\left(z+1\right)=16\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(x+1\right)\left(y+1\right)=4\\\left(y+1\right)\left(z+1\right)=9\\\left(z+1\right)\left(x+1\right)=16\end{cases}}\)
Đặt \(\hept{\begin{cases}x+1=a\\y+1=b\\z+1=c\end{cases}}\)với a,b,c > 1, khi đó ta có
\(\hept{\begin{cases}ab=4\\bc=9\\ca=16\end{cases}}\Leftrightarrow\hept{\begin{cases}abbc=4.9\\c=\frac{9}{b}\\ca=16\end{cases}}\Leftrightarrow\hept{\begin{cases}16b^2=36\\c=\frac{9}{b}\\a=\frac{16}{c}\end{cases}}\Leftrightarrow\hept{\begin{cases}b^2=\frac{36}{16}=\frac{9}{4}\\c=\frac{9}{b}\\a=\frac{16}{c}\end{cases}}\Leftrightarrow\hept{\begin{cases}b=\frac{3}{2}\\c=\frac{9}{\frac{3}{2}}=6\\a=\frac{16}{6}=\frac{8}{3}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=a-1=\frac{8}{3}-1=\frac{5}{3}\\y=b-1=\frac{3}{2}-1=\frac{1}{2}\\z=c-1=6-1=5\end{cases}}\)
Vậy \(P=x+y+z=\frac{5}{3}+\frac{1}{2}+5=\frac{10+3+30}{6}=\frac{43}{6}\)

Bài 5:
1) Ta có: \(2x\left(x+1\right)-2x^2-2x\)
\(=2x^2+2x-2x^2-2x\)
=0
2) Ta có: \(3x\left(x-2\right)-3\left(x^2-2x\right)+4\)
\(=3x^2-6x-3x^2+6x+4\)
=4
3) Ta có: \(\left(x-1\right)\left(x-5\right)-x^2+6x-5\)
\(=x^2-6x+5-x^2+6x-5\)
=0
4) Ta có: \(\left(2x+1\right)\left(x-1\right)-2x^2+x-5\)
\(=2x^2-2x+x-1-2x^2+x-5\)
=-6
5) Ta có: \(\left(3x-2\right)\left(x-1\right)-3x^2+5x-4\)
\(=3x^2-3x-2x+2-3x^2+5x-4\)
=-2
6) Ta có: \(2x\left(x+1\right)-x\left(x+3\right)-x^2+x+5\)
\(=2x^2+2x-x^2-3x-x^2+x+5\)
=5

Bài 1:
a: \(=-10x^3+20x^4-5x\)
b: \(=\dfrac{1}{3}a^2b+7a^5-1\)
c: \(=a^3+8+25-a^3=33\)
d: \(=x^2-16+8-x^3=-x^3+x^2-8\)
e: \(=a^3+1+8-a^3=9\)
f: \(=\dfrac{7-2x+4x-8}{2x+3}=\dfrac{2x-1}{2x+3}\)
g: \(=\dfrac{3}{2\left(x+3\right)}-\dfrac{2}{x\left(x+3\right)}\)
\(=\dfrac{3x-4}{2x\left(x+3\right)}\)




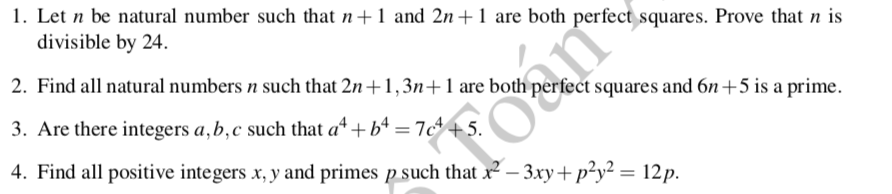



Câu 4:
Xét tam giác ABC có
D là trung điểm của AC(gt)
E là trung điểm của BC(gt)
=> DE là đường trung bình của tam giác ABC
\(\Rightarrow AB=2DE=2.15=30\left(m\right)\)
Câu 5:
Xét hình thang ABCD có:
E là trung điểm của AD(gt)
F là trung điểm của BC(gt)
=> EF là đường trung bình của hình thang ABCD
\(\Rightarrow EF=\dfrac{AB+CD}{2}\Rightarrow45=\dfrac{32+x}{2}\Rightarrow x=45.2-32=58\left(cm\right)\)
Câu 6:
Xét hình thang AMEC có:
B là trung điểm AC(AB=BC)
BN//CE//AM( cùng vuông góc AD)
=> N là trung điểm ME
=> ME=2.MN=70(cm)
Xét hình thang BNFD có:
C là trung điểm BD(BC=CD)
CE//BN//DF(cùng vuông góc AD)
=> E là trung điểm NF
=> EF=EN=MN=35cm
Ta có: MF = EF+ME=70+35=105(cm)
Câu 5:
Hình thang ABCD có
E là trung điểm của AD
F là trung điểm của BC
Do đó: EF là đường trung bình của hình thang ABCD
Suy ra: \(EF=\dfrac{AB+CD}{2}\)
\(\Leftrightarrow x+32=90\)
hay x=58cm