Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=180^0\)
Do đó: MAOB là tứ giác nội tiếp

Lời giải:
$A=1+\frac{1}{\sqrt{x}-3}$
Để $A$ max thì $\sqrt{x}-3$ phải dương và nhỏ nhất.
Với $x$ nguyên, để $\sqrt{x}-3$ dương và nhỏ nhất thì $x=10$
Khi đó, $A_{\max}=1+\frac{1}{\sqrt{10}-3}=4+\sqrt{10}$
------------------
$B=1+\frac{1}{\sqrt{x}-2}$.
Lập luận tương tự phần a, ta thấy với $x$ nguyên không âm thì $\sqrt{x}-2$ đạt giá trị dương nhỏ nhất tại $x=5$
$\Rightarrow B_{\max}=1+\frac{1}{\sqrt{5}-2}=3+\sqrt{5}$

3) Ta có: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\cdot1\cdot\left(m^2-6\right)\)
\(=\left(2m-2\right)^2-4\left(m^2-6\right)\)
\(=4m^2-8m+4-4m^2+24\)
\(=-8m+28\)
Để phương trình có hai nghiệm phân biệt x1;x2 thì Δ>0
\(\Leftrightarrow-8m+28>0\)
\(\Leftrightarrow-8m>-28\)
hay \(m< \dfrac{7}{2}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{1}=2m-2\\x_1x_2=m^2-6\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2=16\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=16\)
\(\Leftrightarrow\left(2m-2\right)^2-2\left(m^2-6\right)-16=0\)
\(\Leftrightarrow4m^2-8m+4-2m^2+12-16=0\)
\(\Leftrightarrow2m^2-8m=0\)
\(\Leftrightarrow2m\left(m-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\left(nhận\right)\\m=4\left(loại\right)\end{matrix}\right.\)


ĐK: \(x\le3\)
Đặt \(a=\sqrt{3-x}\left(a\ge0\right)\) \(\Leftrightarrow3-a^2=x\)
Pttt: \(x^3+\left(3-a^2\right)\left(1+a\right)=4a\)
\(\Leftrightarrow x^3-a^3-a^2-a+3=0\)
\(\Leftrightarrow x^3-a^3+\left(3-a^2\right)-a=0\)
\(\Leftrightarrow\left(x-a\right)\left(x^2+ax+a^2\right)+\left(x-a\right)=0\)
\(\Leftrightarrow x-a=0\) \(\Leftrightarrow x=a\) \(\Leftrightarrow x=\sqrt{3-x}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x^2=3-x\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x^2+x-3=0\end{matrix}\right.\)\(\Rightarrow x=\dfrac{-1+\sqrt{13}}{2}\)(thỏa)
Vậy...



ĐKXĐ:\(x>-3\)
\(\sqrt{x}+\sqrt{x+3}=x+4\)\(\Leftrightarrow x+x+3+2\sqrt{x}\sqrt{x+3}=\left(x+4\right)^2\)
\(\Leftrightarrow2x+3+2\sqrt{x^2+3x}=x^2+8x+16\)
\(\Leftrightarrow x^2+8x+16-2x-3-2\sqrt{x^2+3x}=0\)
\(\Leftrightarrow\left(x^2+3x-2\sqrt{x^2+3x}+1\right)+3x+12=0\)
\(\Leftrightarrow\left(\sqrt{x^2+3x}-1\right)^2+3\left(x+4\right)=0\)
Ta thấy:\(\hept{\begin{cases}\left(\sqrt{x^2+3x}-1\right)^2\ge0\\x>-3\Leftrightarrow3\left(x+4\right)>0\end{cases}}\)
\(\Rightarrow\left(\sqrt{x^2+3x}-1\right)^2+3\left(x+4\right)>0\)
\(\Leftrightarrow x\in\varnothing\)
Vậy phương trình vô nghiệm.




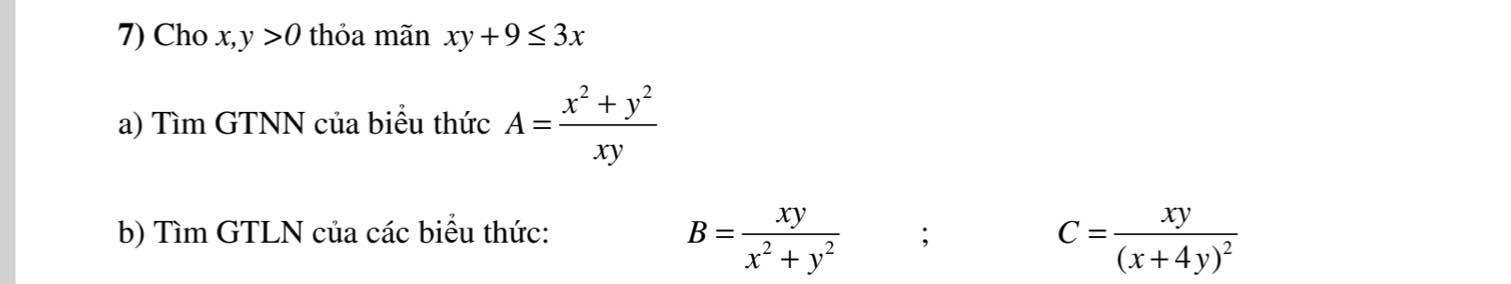 mọi người giúp em 2 ý này với ạ, em rất cảm ơn ạ 🥺
mọi người giúp em 2 ý này với ạ, em rất cảm ơn ạ 🥺