
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\dfrac{20^{10}+1}{20^{10}-1}=1-\dfrac{2}{20^{10}-1}\)
\(B=\dfrac{20^{10}-1}{20^{10}-3}=1-\dfrac{2}{20^{10}-3}\)
Do đó: A>B

a: Xét ΔABD và ΔHBD có
BA=BH
\(\widehat{ABD}=\widehat{HBD}\)
BD chung
Do đó: ΔABD=ΔHBD
b: Ta có: ΔABD=ΔHBD
nên \(\widehat{BAD}=\widehat{BHD}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BHD}=90^0\)
hay DH\(\perp\)BC

bài này mk bt lm nhưng mk đag trog trạng thái mệt mỏi nên ngại lắm, để lúc nào rảnh mk giúp bn nhé!


a) \(\Rightarrow\left(x-3\right)\left(x+4\right)=5.12\)
\(\Rightarrow x^2+x-72=0\)
\(\Rightarrow\left(x-8\right)\left(x+9\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=8\\x=-9\end{matrix}\right.\)
b) \(\Rightarrow\left(x+3\right)^2=36\)
\(\Rightarrow\left[{}\begin{matrix}x+3=6\\x+3=-6\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-9\end{matrix}\right.\)
c) \(\Rightarrow2x^2=8\Rightarrow x^2=4\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)

Bạn cần bài nào ạ? Nếu bạn cần giúp tất cả thì bạn tách ra từng CH khác nhau nhé!

a, Ta co góc BAD + góc ADC = 180 độ
mà góc ở vị trí trong cùng phía
=> AB//DC
b, Ta có góc ABC + góc xBC = 180 độ ( kề bù)
=> góc ABC = 180 - góc xBC = 180 -32 =148 độ
Ta có AB // DC hay Ax//DC
=> góc xBC = góc BCD = 32 độ ( sole trong)
a, Ta có \(\widehat{BAD}\) + \(\widehat{ADC}\) = 180 độ
mà 2 góc này ở vị trí trong cùng phía của AD cắt AB và CD
=> AB//DC
b, Ta có \(\widehat{ABC}\) + \(\widehat{xBC}\) = 180 độ ( kề bù)
=> \(\widehat{ABC}\) = 180 - \(\widehat{xBC}\) = 180 -32 =\(148^0\)
Ta có AB // DC hay Ax//DC
=> \(\widehat{xBC}\) = \(\widehat{BCD}\) = \(32^0\) ( so le trong)

5:
a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
AB=AC
góc A chung
=>ΔAEB=ΔAFC
b: AF=AE
=>BF=CE
Xét ΔAFI vuông tại F và ΔAEI vuông tại E có
AI chung
AF=AE
=>ΔAFI=ΔAEI
=>góc FAI=góc EAI
=>AI là phân giác của góc BAC
d: AE=căn 10^2-6^2=8cm

10.
\(H\left(x\right)=-5x^4+10x^3-15x+1\)
\(=-5x\left(x^3-2x^2+3\right)+1\)
\(=-5x.0+1\)
\(=1\)
9.
\(P\left(x\right)-Q\left(x\right)=\left(1-a\right)x^3+x^2+x-6\)
\(P\left(x\right)-Q\left(x\right)\) là đa thức bậc 3 khi và chỉ khi \(1-a\ne0\)
\(\Rightarrow a\ne1\)
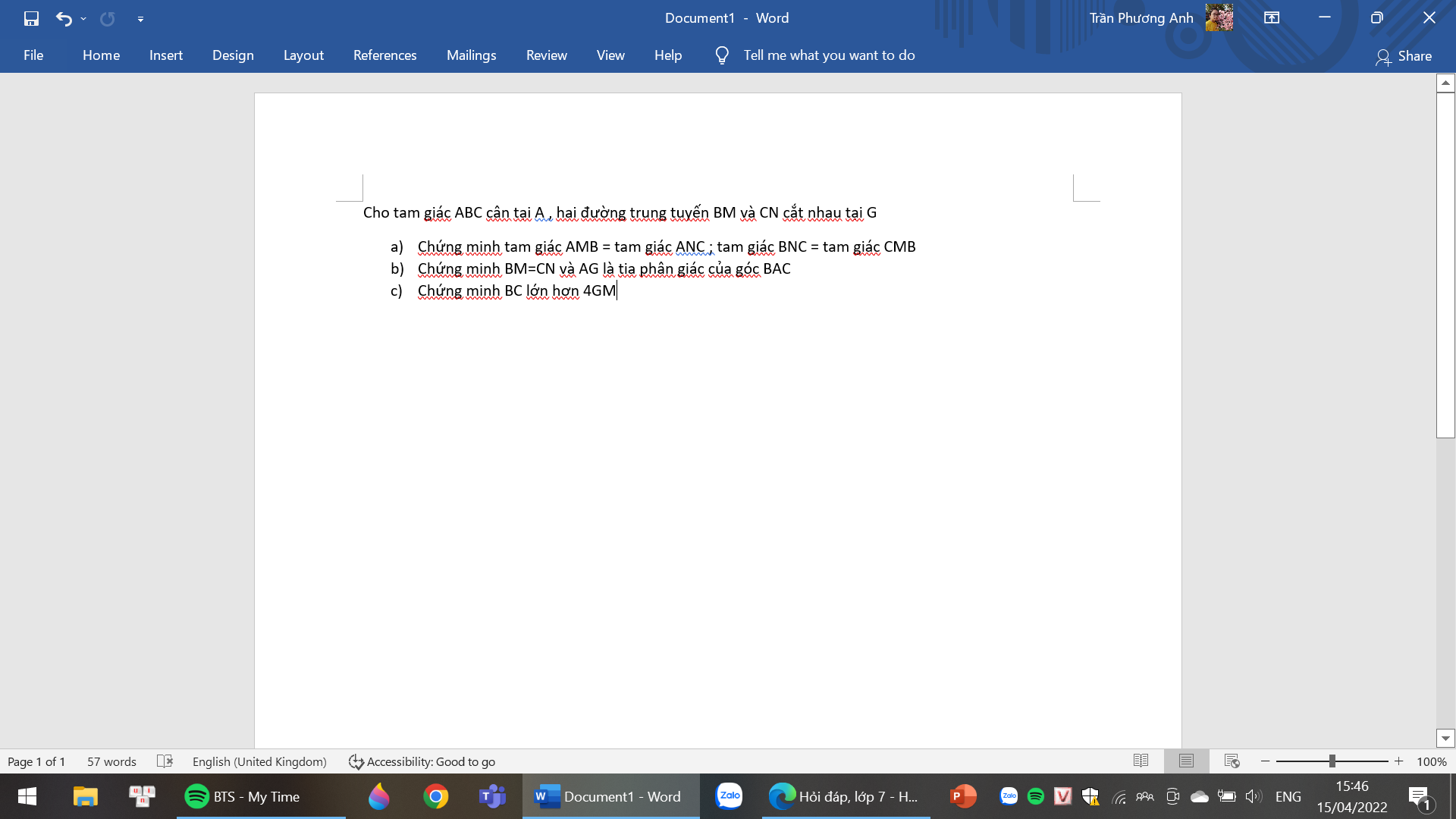



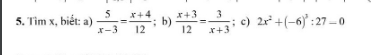





a: Xét ΔAMB và ΔANC có
AM=AN
\(\widehat{BAM}\) chung
AB=AC
Do đó: ΔAMB=ΔANC
Xét ΔBNC và ΔCMB có
NB=MC
BC chung
NC=MB
Do đó: ΔBNC=ΔCMB
b: Ta có: ΔABM=ΔACN
nên BM=CN
Xét ΔGBC có \(\widehat{GBC}=\widehat{GCB}\)
nên ΔGBC cân tại G
Xét ΔABG và ΔACG có
AB=AC
BG=CG
AG chung
Do đó: ΔABG=ΔACG
Suy ra: \(\widehat{BAG}=\widehat{CAG}\)
hay AG là tia phân giác của góc BAC
cảm ơn bạn rất nhiều ^.^