
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
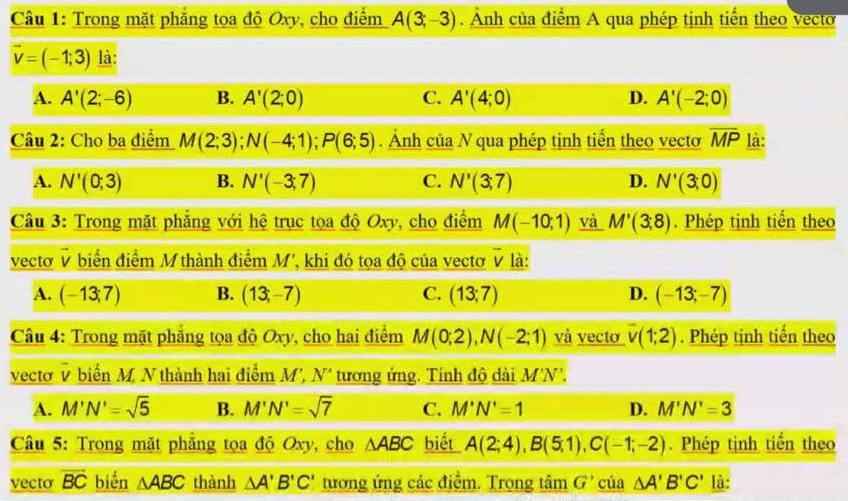
\(\left\{{}\begin{matrix}x_{A'}=x_A+\left(-1\right)=2\\y_{A'}=y_A+3=0\end{matrix}\right.\) \(\Rightarrow A'\left(2;0\right)\)
2.
\(\overrightarrow{MP}=\left(4;2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_{N'}=x_N+4=-4+4=0\\y_{N'}=y_N+2=1+2=3\end{matrix}\right.\)
\(\Rightarrow N'\left(0;3\right)\)
3.
\(\overrightarrow{MM'}=\left(13;7\right)\Rightarrow\overrightarrow{v}=\overrightarrow{MM'}=\left(13;7\right)\)
4.
\(\overrightarrow{MN}=\left(-2;-1\right)\Rightarrow MN=\sqrt{\left(-2\right)^2+\left(-1\right)^2}=\sqrt{5}\)
\(\Rightarrow M'N'=MN=\sqrt{5}\)
5.
Gọi G là trọng tâm ABC \(\Rightarrow G\left(2;1\right)\)
\(\overrightarrow{BC}=\left(-6;-3\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_{G'}=2-6=-4\\y_{G'}=1-3=-2\end{matrix}\right.\) \(\Rightarrow G'\left(-4;-2\right)\)

Câu 1: Ý C
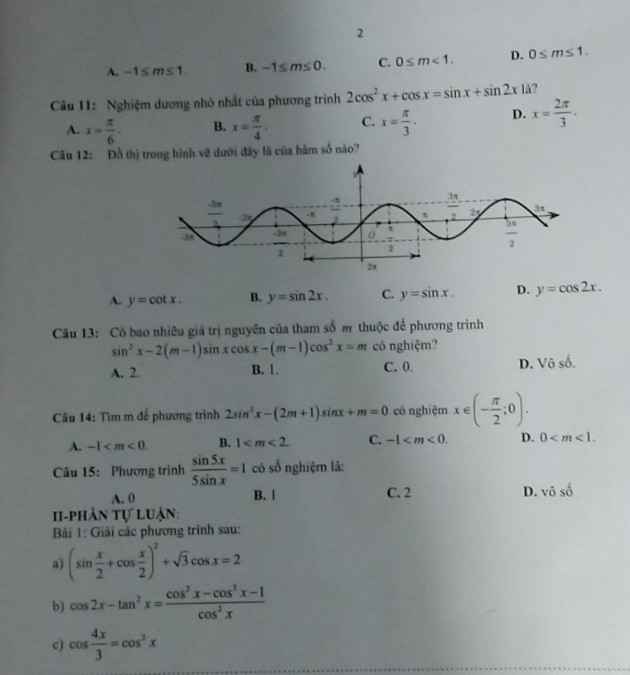
PT \(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\) mà\(x\in\left(0;2\pi\right)\)
Có 3 nghiệm
Câu 2: Ý A
PT \(\Leftrightarrow\left[{}\begin{matrix}sinx=1\\sinx=\dfrac{1}{2}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\) mà \(0\le x< \dfrac{\pi}{2}\)
\(\Rightarrow x=\dfrac{\pi}{6}\)

\(\dfrac{4kq.x}{\sqrt{\left(x^2+a^2\right)^3}}=\dfrac{4kq.x}{\sqrt{\left(x^2+\dfrac{a^2}{2}+\dfrac{a^2}{2}\right)^3}}\le\dfrac{4kq.x}{\sqrt{\dfrac{27.x^2.a^4}{4}}}=\dfrac{4kq.x}{\dfrac{3\sqrt{3}}{2}.x.a^2}=\dfrac{8\sqrt{3}.kq}{9a^2}\)
Dấu "=" xảy ra khi \(x=\dfrac{a}{\sqrt{2}}\)

\(IM=\dfrac{1}{4}IB\Rightarrow IM=\dfrac{1}{5}BM\Rightarrow\overrightarrow{MI}=\dfrac{1}{5}\overrightarrow{MB}=-\dfrac{1}{10}\left(\overrightarrow{BC}+\overrightarrow{BD}\right)\)
\(\Rightarrow\overrightarrow{DI}=\overrightarrow{DM}+\overrightarrow{MI}=\dfrac{1}{2}\overrightarrow{DC}-\dfrac{1}{10}\left(\overrightarrow{BC}+\overrightarrow{BD}\right)=\dfrac{1}{2}\overrightarrow{DB}+\dfrac{1}{2}\overrightarrow{BC}-\dfrac{1}{10}\overrightarrow{BC}-\dfrac{1}{10}\overrightarrow{BD}\)
\(\Rightarrow\overrightarrow{DI}=\dfrac{2}{5}\overrightarrow{BC}-\dfrac{3}{5}\overrightarrow{BD}\)
\(\overrightarrow{DJ}=\overrightarrow{DC}+\overrightarrow{CJ}=\overrightarrow{DB}+\overrightarrow{BC}+x.\overrightarrow{CB}=\left(1-x\right)\overrightarrow{BC}-\overrightarrow{BD}\)
D; I; J thẳng hàng \(\Rightarrow\dfrac{1-x}{\dfrac{2}{5}}=\dfrac{1}{\dfrac{3}{5}}\Rightarrow x=\dfrac{1}{3}\)
\(\Rightarrow CJ=\dfrac{1}{3}CB\Rightarrow BJ=\dfrac{2}{3}BC\Rightarrow\dfrac{BJ}{BC}=\dfrac{2}{3}\)
Gọi N là trung điểm AD \(\Rightarrow\dfrac{BG}{BN}=\dfrac{2}{3}\) (theo t/c trọng tâm)
\(\Rightarrow\dfrac{BJ}{BC}=\dfrac{BG}{BN}\Rightarrow JG||CN\)
\(\Rightarrow\widehat{\left(JG;CD\right)}=\widehat{\left(CN;CD\right)}=\widehat{NCD}=30^0\) (do tam giác ACD đều)


1. Quá dài
2. Quá mờ, không thể đọc được, đặc biệt là phần 2
Em nên chụp lại cho rõ hơn và chia nhỏ ra

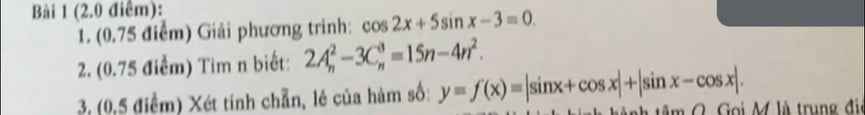





 mọi người giải giúp em theo phương pháp tự luận với ạ
mọi người giải giúp em theo phương pháp tự luận với ạ 






1.1
\(cos2x+5sinx-3=0\)
\(\Leftrightarrow1-2sin^2x+5sinx-3=0\)
\(\Leftrightarrow2sin^2x-5sinx+2=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sinx-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\\sinx=2\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)