
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


đặt M là n^3 -9n^2+2n.
TH1 : n có dạng 2k => M chia hết cho 2 (bạn tự cm)
TH2 ; n có dạng 2k+1 => M = (2k+1)^3-9(2k+1)^2+2n
=8k^3+6k+12k^2+1-9(4k^2+4k+1)+2n = ... => M chia hết cho 2 với mọi n (1)
Xét n có dạng 3k => M chia hết cho 3
Xét n có dạng 3k+1 => n^3+2n=(3k+1)^3+2(3k+1)=27k^3+9k+27k^2+6k+3 chia hết cho 3 mà 9n^2 cũng chia hết cho 3 => M chia hết cho 3
Tương tự bạn xét n =3k+2....
=> M chia hết cho 3 vs mọi n (2)
Từ (1) và (2) => M chia hết cho 6

Câu 10:
a: ĐKXĐ: \(\left\{{}\begin{matrix}x\notin\left\{2;-1\right\}\\y\ne-5\end{matrix}\right.\)
\(A=\dfrac{y+5}{x^2-4x+4}\cdot\dfrac{x^2-4}{x+1}\cdot\dfrac{x-2}{y+5}\)
\(=\dfrac{y+5}{y+5}\cdot\dfrac{\left(x^2-4\right)}{x^2-4x+4}\cdot\dfrac{x-2}{x+1}\)
\(=\dfrac{\left(x^2-4\right)\cdot\left(x-2\right)}{\left(x+1\right)\left(x^2-4x+4\right)}\)
\(=\dfrac{\left(x+2\right)\left(x-2\right)\cdot\left(x-2\right)}{\left(x+1\right)\left(x-2\right)^2}=\dfrac{x+2}{x+1}\)
b: \(A=\dfrac{x+2}{x+1}\)
=>A không phụ thuộc vào biến y
Khi x=1/2 thì \(A=\left(\dfrac{1}{2}+2\right):\left(\dfrac{1}{2}+1\right)=\dfrac{5}{2}:\dfrac{3}{2}=\dfrac{5}{2}\cdot\dfrac{2}{3}=\dfrac{5}{3}\)
Câu 12:
a: \(A=\dfrac{x}{x+3}+\dfrac{2x}{x-3}+\dfrac{9-3x^2}{x^2-9}\)
\(=\dfrac{x}{x+3}+\dfrac{2x}{x-3}+\dfrac{9-3x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{x\left(x-3\right)+2x\left(x+3\right)+9-3x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{x^2-3x+2x^2+6x+9-3x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{3x+9}{\left(x+3\right)\left(x-3\right)}=\dfrac{3\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}=\dfrac{3}{x-3}\)
b: Khi x=1 thì \(A=\dfrac{3}{1-3}=\dfrac{3}{-2}=-\dfrac{3}{2}\)
\(x+\dfrac{1}{3}=\dfrac{10}{3}\)
=>\(x=\dfrac{10}{3}-\dfrac{1}{3}\)
=>\(x=\dfrac{9}{3}=3\left(loại\right)\)
Vậy: Khi x=3 thì A không có giá trị
c: \(B=A\cdot\dfrac{x-3}{x^2-4x+5}\)
\(=\dfrac{3}{x-3}\cdot\dfrac{x-3}{x^2-4x+5}\)
\(=\dfrac{3}{x^2-4x+5}\)
\(x^2-4x+5=x^2-4x+4+1=\left(x-2\right)^2+1>=1\forall x\) thỏa mãn ĐKXĐ
=>\(B=\dfrac{3}{x^2-4x+5}< =\dfrac{3}{1}=3\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi x-2=0
=>x=2

Cái này bạn vẽ hình nhé, mình chỉ giải thôi mình ko có nhiều tg.
a)Có:
ABC+ABx=180°(hai góc kề bù)
=>ABx=180°-80°
=>ABx=100°
Có:
ABI=IBx=ABx:2(BI là pg ABx)
=>ABI=IBx=100°:2:50°
Có:CBA+ABI=CBI(hai góc kề bù)
=>CBI=80°+50°=130°
Có CI là pg của góc C
=>ACI=BCI=C:2
=>ACI=BCI=40°:2=20°
b)Có:
ABx=A+ACB(tc góc ngoài tam giác)
=>A=ABx-ACB=2IBx-2ICB
=2(IBx-ICB) (1)
Có:
IBx=I+ICB(tc góc ngoài tam giác)
=>I=IBx-ICB (2)
Từ (1) và (2)
=>đpcm
Linh ơi! Làm đúng rồi :). Nếu trình bày rõ ràng dễ đọc hơn nữa càng tốt chứ cô check bài mà mắt cứ xoay vòng :)).
Bài bên dưới chỉ chỉnh sửa lại theo đúng hướng của bạn Linh.
a ) ^ABx là góc ngoài của \(\Delta\)ABC tại đỉnh B.
=> ^ABx = 180\(^o\)- ^ABC = 180\(^o\)- 80\(^o\)= 100\(^o\).
Có BI là phân giác ^ABx
=> ^ABI = ^ABx : 2 = 100\(^o\):2 = 50\(^o\).
Ta lại có: ^CBI = ^CBA + ^ABI = 80\(^o\)+ 50\(^o\)= 130\(^o\)
Có CI là phân giác ^BCA
=> ^ BCI = ^BCA : 2 = 40\(^o\): 2 = 20\(^o\).
b/ Chứng minh tổng quát.
Có: ^IBx là góc ngoài của \(\Delta\)IBC tại đỉnh B.
=> ^IBx = ^ICB + ^BIC => ^BIC = ^IBx - ^ICB (1)
Ta có : ^ABx là góc ngoài của \(\Delta\)ABC tại đỉnh B.
=> ^ABx = ^ACB + ^BAC => ^BAC = ^ABx - ^BCA = 2. ^IBx - 2. ^ICB ( chỗ này sử dụng phân giác nhé!)
= 2 ( ^IBx - ^ICB ) = 2. ^BIC ( theo (1))
=> ^BAC = 2. ^BIC

Hướng dẫn: A đạt GTLN khi \(\dfrac{1}{A}\) đạt GTNN
Ta có: \(x^2+2\ge0\forall x\)
\(\Rightarrow A=\dfrac{1}{x^2+2}\le\dfrac{1}{2}\forall x\)
Vậy GTLN của A là 1/2
=> A


-Bài 3:
2) -Áp dụng BĐT Caushy Schwarz ta có:
\(A=\dfrac{1}{x^3+3xy^2}+\dfrac{1}{y^3+3x^2y}\ge\dfrac{\left(1+1\right)^2}{x^3+3xy^2+3x^2y+y^3}=\dfrac{4}{\left(x+y\right)^3}\ge\dfrac{4}{1^3}=4\)-Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)

Câu 1: A
Câu 2: B
Câu 3: D
Câu 4: A
Câu 5: C
Câu 6: B
Câu 7: A
Câu 9: B

\(a,a^2-10a+25=\left(a-5\right)^2\\ b,4x^2+4x+1=\left(2x+1\right)^2\\ c,4x^2-9=\left(2x-3\right)\left(2x+3\right)\\ d,x^3+3x^2+3x+1=\left(x+1\right)^3\\ e,a^3-3a^2b+3ab^2-b^3=\left(a-b\right)^3\\ f,y^3+8=\left(y+2\right)\left(y^2-2y+4\right)\\ g,27x^3-1=\left(3x-1\right)\left(9x^2+3x+1\right)\)
\(a^2-10x+25=\left(a-5\right)^2\)
b/ \(4x^2+4x+1=\left(2x+1\right)^2\)
c/ \(4b^2-9=\left(2b-3\right)\left(2b+3\right)\)
d/ \(x^3+3x^2+3x+1=\left(x+1\right)^3\)
e/ \(a^3-3a^2b+3ab^2-b^3=\left(a-b\right)^3\)
f/ \(y^3+8=\left(y+2\right)\left(y^2-2y+4\right)\)
g/ \(27x^3-1=\left(3x-1\right)\left(9x^2+3x+1\right)\)

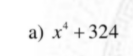








\(x^4+324=\left(x^4+36x^2+324\right)-36x^2\)
\(=\left(x^2+18\right)^2-36x^2\)
\(=\left(x^2-6x+18\right)\left(x^2+6x+18\right)\)
Đây là dùng CT thêm và bớt phải ko cậu